Cfxtrjtrk

本条目需要擴充。（2017年6月27日） 请協助改善这篇條目，更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。

常態分布

紅線代表標準常態分佈 概率密度函數
顏色與機率密度函數同 累積分佈函數
參數	μ{displaystyle mu }数学期望（实数） σ2>0{displaystyle sigma ^{2}>0}方差（实数）
支撑集	x∈(−∞;+∞){displaystyle xin (-infty ;+infty )!}
概率密度函数	1σ2πexp⁡(−(x−μ)22σ2){displaystyle {frac {1}{sigma {sqrt {2pi }}}};exp left(-{frac {left(x-mu right)^{2}}{2sigma ^{2}}}right)!}
累積分佈函數	12(1+erf⁡x−μσ2){displaystyle {frac {1}{2}}left(1+operatorname {erf} {frac {x-mu }{sigma {sqrt {2}}}}right)!}
期望值	μ{displaystyle mu }
中位數	μ{displaystyle mu }
眾數	μ{displaystyle mu }
方差	σ2{displaystyle sigma ^{2}}
偏度	0
峰度	0
信息熵	ln⁡(σ2πe){displaystyle ln left(sigma {sqrt {2,pi ,e}}right)!}
動差生成函數	MX(t)=exp⁡(μt+σ2t22){displaystyle M_{X}(t)=exp left(mu ,t+sigma ^{2}{frac {t^{2}}{2}}right)}
特性函数	ϕX(t)=exp⁡(μit−σ2t22){displaystyle phi _{X}(t)=exp left(mu ,i,t-{frac {sigma ^{2}t^{2}}{2}}right)}

常態分布（英语：normal distribution）又名高斯分布（英语：Gaussian distribution），是一個非常常見的連續機率分布。常態分布在统计学上十分重要，經常用在自然和社会科学來代表一個不明的隨機變量。^[1][2]

若隨機變量X{displaystyle X}服從一個位置參數為μ{displaystyle mu }、尺度參數為σ{displaystyle sigma }的常態分布，記為：

X∼N(μ,σ2),{displaystyle Xsim N(mu ,sigma ^{2}),}^[3]

則其機率密度函數為

f(x)=1σ2πe−(x−μ)22σ2{displaystyle f(x)={1 over sigma {sqrt {2pi }}},e^{-{(x-mu )^{2} over 2sigma ^{2}}}}^[3]

常態分布的數學期望值或期望值μ{displaystyle mu }等於位置參數，決定了分布的位置；其方差σ2{displaystyle sigma ^{2}}的開平方或標準差σ{displaystyle sigma }等於尺度參數，決定了分布的幅度。

常態分布的機率密度函數曲線呈鐘形，因此人們又經常稱之為鐘形曲線（类似于寺庙里的大钟，因此得名）。我們通常所說的標準常態分布是位置參數μ=0{displaystyle mu =0}，尺度參數σ2=1{displaystyle sigma ^{2}=1}的常態分布^[3]（見右圖中紅色曲線）。

概要

常態分布是自然科學與行為科學中的定量現象的一個方便模型。各種各樣的心理學測試分數和物理現象比如光子計數都被發現近似地服從常態分布。儘管這些現象的根本原因經常是未知的，理論上可以證明如果把許多小作用加起來看做一個變量，那麼這個變量服從常態分布（在R.N.Bracewell的Fourier transform and its application中可以找到一種簡單的證明）。常態分布出現在許多區域統計：例如，採樣分布均值是近似地常態的，即使被採樣的樣本的原始群體分布並不服從常態分布。另外，常態分布信息熵在所有的已知均值及方差的分布中最大，這使得它作為一種均值以及方差已知的分布的自然選擇。常態分布是在統計以及許多統計測試中最廣泛應用的一類分布。在概率論，常態分布是幾種連續以及離散分布的極限分布。

歷史

常態分布最早是棣莫弗在1718年著作的書籍的（Doctrine of Change），及1734年發表的一篇關於二項分布文章中提出的，當二項隨機變數的位置參數n很大及形狀參數p為1/2時，則所推導出二項分布的近似分布函數就是常態分布。拉普拉斯在1812年发表的《分析概率论》（Theorie Analytique des Probabilites）中對棣莫佛的結論作了擴展到二項分布的位置參數為n及形狀參數為1>p>0時。現在这一结论通常被稱為棣莫佛－拉普拉斯定理。

拉普拉斯在誤差分析試驗中使用了常態分布。勒讓德於1805年引入最小二乘法這一重要方法；而高斯則宣稱他早在1794年就使用了該方法，並通過假設誤差服從常態分布給出了嚴格的證明。

「鐘形曲線」這個名字可以追溯到Jouffret他在1872年首次提出這個術語"鐘形曲面"，用來指代二元常態分布（bivariate normal）。正态分布這個名字還被Charles S. Peirce、Francis Galton、Wilhelm Lexis在1875分别獨立地使用。這個術語是不幸的，因為它反映和鼓勵了一種謬誤，即很多概率分布都是常態的。（請參考下面的「實例」）

這個分布被稱為「常態」或者「高斯」正好是Stigler名字由來法則的一個例子，這個法則說「沒有科學發現是以它最初的發現者命名的」。

正态分布的定義

有幾種不同的方法用來說明一個隨機變量。最直觀的方法是概率密度函數，這種方法能夠表示隨機變量每個取值有多大的可能性。累積分布函數是一種概率上更加清楚的方法，請看下邊的例子。還有一些其他的等價方法，例如cumulant、特徵函數、動差生成函數以及cumulant-生成函數。這些方法中有一些對於理論工作非常有用，但是不夠直觀。請參考關於概率分布的討論。

概率密度函數

四个不同参数集的概率密度函数（紅色线代表标准正态分布）

常態分布的概率密度函數均值為μ{displaystyle mu } 方差為σ2{displaystyle sigma ^{2}} (或標準差σ{displaystyle sigma })是高斯函數的一個實例：

f(x;μ,σ)=1σ2πexp⁡(−(x−μ)22σ2){displaystyle f(x;mu ,sigma )={frac {1}{sigma {sqrt {2pi }}}},exp left(-{frac {(x-mu )^{2}}{2sigma ^{2}}}right)}。

(請看指數函數以及π{displaystyle pi }.)

如果一個隨機變量X{displaystyle X}服從這個分布，我們寫作
X{displaystyle X} ~ N(μ,σ2){displaystyle N(mu ,sigma ^{2})}.
如果μ=0{displaystyle mu =0}並且σ=1{displaystyle sigma =1}，這個分布被稱為標準正态分布，這個分布能夠簡化為

f(x)=12πexp⁡(−x22){displaystyle f(x)={frac {1}{sqrt {2pi }}},exp left(-{frac {x^{2}}{2}}right)}。

右邊是給出了不同參數的正态分布的函數圖。

正态分布中一些值得注意的量：

• 密度函數關於平均值對稱


• 平均值與它的眾數（statistical mode）以及中位數（median）同一數值。


• 函數曲線下68.268949%的面積在平均數左右的一個標準差範圍內。


• 95.449974%的面積在平均數左右兩個標準差2σ{displaystyle 2sigma }的範圍內。


• 99.730020%的面積在平均數左右三個標準差3σ{displaystyle 3sigma }的範圍內。


• 99.993666%的面積在平均數左右四個標準差4σ{displaystyle 4sigma }的範圍內。


• 函數曲線的拐點（inflection point）為離平均數一個標準差距離的位置。

累積分布函數

上图所示的機率密度函数的累積分布函數

累積分布函數是指隨機變數X{displaystyle X}小於或等於x{displaystyle x}的機率，用機率密度函數表示為

F(x;μ,σ)=1σ2π∫−∞xexp⁡(−(t−μ)22σ2 )dt.{displaystyle F(x;mu ,sigma )={frac {1}{sigma {sqrt {2pi }}}}int _{-infty }^{x}exp left(-{frac {(t-mu )^{2}}{2sigma ^{2}}} right),dt.}

常態分布的累積分布函数能够由一個叫做误差函数的特殊函数表示：

Φ(z)=12[1+erf⁡(z−μσ2)].{displaystyle Phi (z)={frac {1}{2}}left[1+operatorname {erf} left({frac {z-mu }{sigma {sqrt {2}}}}right)right].}

標準常態分布的累積分布函數習慣上記為Φ{displaystyle Phi }，它僅僅是指μ=0{displaystyle mu =0}，σ=1{displaystyle sigma =1}時的值，

Φ(x)=F(x;0,1)=12π∫−∞xexp⁡(−t22)dt.{displaystyle Phi (x)=F(x;0,1)={frac {1}{sqrt {2pi }}}int _{-infty }^{x}exp left(-{frac {t^{2}}{2}}right),dt.}

將一般常態分布用誤差函數表示的公式简化，可得：

Φ(z)=12[1+erf⁡(z2)].{displaystyle Phi (z)={frac {1}{2}}left[1+operatorname {erf} left({frac {z}{sqrt {2}}}right)right].}

它的反函數被稱為反誤差函數，為：

Φ−1(p)=2erf−1⁡(2p−1).{displaystyle Phi ^{-1}(p)={sqrt {2}};operatorname {erf} ^{-1}left(2p-1right).}

該分位數函數有時也被稱為probit函數。probit函數已被證明沒有初等原函数。

常態分布的分布函數Φ(x){displaystyle Phi (x)}沒有解析表達式，它的值可以通過數值積分、泰勒級數或者漸進序列近似得到。

生成函數

矩母函数

動差生成函數或矩生成函數或動差產生函數被定義為exp⁡(tX){displaystyle exp(tX)}的期望值。

常態分布的動差產生函數如下：

MX(t){displaystyle M_{X}(t),}	=E(etX){displaystyle =mathrm {E} left(e^{tX}right)}
	=∫−∞∞1σ2πe(−(x−μ)22σ2)etxdx{displaystyle =int _{-infty }^{infty }{frac {1}{sigma {sqrt {2pi }}}}e^{left(-{frac {(x-mu )^{2}}{2sigma ^{2}}}right)}e^{tx},dx}
	=e(μt+σ2t22){displaystyle =e^{left(mu t+{frac {sigma ^{2}t^{2}}{2}}right)}}

可以通過在指數函數內配平方得到。

特徵函數

特徵函數被定義為exp⁡(itX){displaystyle exp(itX)}的期望值，其中i{displaystyle i}是虛數單位.
對於一個常态分布來講，特徵函數是：

ϕX(t;μ,σ){displaystyle phi _{X}(t;mu ,sigma )!}	=E[exp⁡(itX)]{displaystyle =mathrm {E} left[exp(itX)right]}
	=∫−∞∞1σ2πexp⁡(−(x−μ)22σ2)exp⁡(itx)dx{displaystyle =int _{-infty }^{infty }{frac {1}{sigma {sqrt {2pi }}}}exp left(-{frac {(x-mu )^{2}}{2sigma ^{2}}}right)exp(itx),dx}
	=exp⁡(iμt−σ2t22).{displaystyle =exp left(imu t-{frac {sigma ^{2}t^{2}}{2}}right).}

把矩生成函數中的t{displaystyle t}換成it{displaystyle it}就能得到特徵函數。

性質

常態分布的一些性質：

1. 如果X∼N(μ,σ2){displaystyle Xsim N(mu ,sigma ^{2}),}且a{displaystyle a}與b{displaystyle b}是實數，那麼aX+b∼N(aμ+b,(aσ)2){displaystyle aX+bsim N(amu +b,(asigma )^{2})} (參見期望值和方差).


2. 如果X∼N(μX,σX2){displaystyle Xsim N(mu _{X},sigma _{X}^{2})}與Y∼N(μY,σY2){displaystyle Ysim N(mu _{Y},sigma _{Y}^{2})}是統計獨立的常態隨機變量，那麼：
   
   
   
   • 它們的和也滿足常態分布U=X+Y∼N(μX+μY,σX2+σY2){displaystyle U=X+Ysim N(mu _{X}+mu _{Y},sigma _{X}^{2}+sigma _{Y}^{2})} (proof（英语：sum of normally distributed random variables）).
   
   
   • 它們的差也滿足常態分布V=X−Y∼N(μX−μY,σX2+σY2){displaystyle V=X-Ysim N(mu _{X}-mu _{Y},sigma _{X}^{2}+sigma _{Y}^{2})}.
   
   
   • 
     U{displaystyle U}與V{displaystyle V}兩者是相互獨立的。（要求X与Y的方差相等）
   
   
   
   


3. 如果X∼N(0,σX2){displaystyle Xsim N(0,sigma _{X}^{2})}和Y∼N(0,σY2){displaystyle Ysim N(0,sigma _{Y}^{2})}是獨立常態隨機變量，那麼：
   
   
   
   • 它們的積XY{displaystyle XY}服從機率密度函數為p{displaystyle p}的分布
     

     
     p(z)=1πσXσYK0(|z|σXσY),{displaystyle p(z)={frac {1}{pi ,sigma _{X},sigma _{Y}}};K_{0}left({frac {|z|}{sigma _{X},sigma _{Y}}}right),}其中K0{displaystyle K_{0}}是修正貝塞爾函數（modified Bessel function）

     
     
   
   
   • 它們的比符合柯西分布，滿足X/Y∼Cauchy(0,σX/σY){displaystyle X/Ysim mathrm {Cauchy} (0,sigma _{X}/sigma _{Y})}.
   
   
   
   


4. 如果X1,⋯,Xn{displaystyle X_{1},cdots ,X_{n}}為獨立標準常態隨機變量，那麼X12+⋯+Xn2{displaystyle X_{1}^{2}+cdots +X_{n}^{2}}服從自由度為n的卡方分布。

標準化常態隨機變量

動差或矩（moment）

一些常態分布的一階動差如下：

階數	原點矩	中心矩	累積量
0	1	0
1	μ{displaystyle mu }	0	μ{displaystyle mu }
2	μ2+σ2{displaystyle mu ^{2}+sigma ^{2}}	σ2{displaystyle sigma ^{2}}	σ2{displaystyle sigma ^{2}}
3	μ3+3μσ2{displaystyle mu ^{3}+3mu sigma ^{2}}	0	0
4	μ4+6μ2σ2+3σ4{displaystyle mu ^{4}+6mu ^{2}sigma ^{2}+3sigma ^{4}}	3σ4{displaystyle 3sigma ^{4}}	0

標準常態的所有二階以上的累積量為零。

生成常態隨機變量

中心極限定理

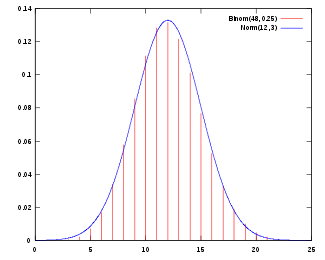
正态分布的概率密度函數，參數為μ = 12，σ = 3，趨近於n = 48、p = 1/4的二項分布的概率質量函數。

常態分布有一個非常重要的性質：在特定條件下，大量統計獨立的隨機變量的平均值的分布趨於正态分布，這就是中心極限定理。中心極限定理的重要意義在於，根據這一定理的結論，其他概率分布可以用正态分布作為近似。

• 
  參數為n{displaystyle n}和p{displaystyle p}的二項分布，在n{displaystyle n}相當大而且p{displaystyle p}接近0.5時近似於正态分布（有的參考書建議僅在np{displaystyle np}與n(1−p){displaystyle n(1-p)}至少為5時才能使用這一近似）。

近似正态分布平均數為μ=np{displaystyle mu =np}且方差為σ2=np(1−p){displaystyle sigma ^{2}=np(1-p)}.

• 
  一泊松分布帶有參數λ{displaystyle lambda }當取樣樣本數很大時將近似正态分布λ{displaystyle lambda }.

近似正态分布平均數為μ=λ{displaystyle mu =lambda }且方差為σ2=λ{displaystyle sigma ^{2}=lambda }.

這些近似值是否完全充分正確取決於使用者的使用需求

無限可分性

正态分布是無限可分的概率分布。

穩定性

正态分布是嚴格穩定的概率分布。

標準偏差

深藍色區域是距平均值小於一個標準差之內的數值範圍。在常態分布中，此範圍所佔比率為全部數值之68%，根據常態分布，兩個標準差之內的比率合起來為95%；三個標準差之內的比率合起來為99%。

在實際應用上，常考慮一組數據具有近似於常態分布的機率分布。若其假設正確，則約68.3%數值分布在距離平均值有1個標準差之內的範圍，約95.4%數值分布在距離平均值有2個標準差之內的範圍，以及約99.7%數值分布在距離平均值有3個標準差之內的範圍。稱為「68-95-99.7法則」或「經驗法則」。

相關分布

• 
  R∼Rayleigh(σ){displaystyle Rsim mathrm {Rayleigh} (sigma )}是瑞利分布，如果R=X2+Y2{displaystyle R={sqrt {X^{2}+Y^{2}}}}，这里X∼N(0,σ2){displaystyle Xsim N(0,sigma ^{2})}和Y∼N(0,σ2){displaystyle Ysim N(0,sigma ^{2})}是两个独立正态分布。


• 
  Y∼χν2{displaystyle Ysim chi _{nu }^{2}}是卡方分布具有ν{displaystyle nu }自由度，如果Y=∑k=1νXk2{displaystyle Y=sum _{k=1}^{nu }X_{k}^{2}}这里Xk∼N(0,1){displaystyle X_{k}sim N(0,1)}其中k=1,…,ν{displaystyle k=1,dots ,nu }是独立的。


• 
  Y∼Cauchy(μ=0,θ=1){displaystyle Ysim mathrm {Cauchy} (mu =0,theta =1)}是柯西分布，如果Y=X1/X2{displaystyle Y=X_{1}/X_{2}}，其中X1∼N(0,1){displaystyle X_{1}sim N(0,1)}并且X2∼N(0,1){displaystyle X_{2}sim N(0,1)}是两个独立的正态分布。


• 
  Y∼Log-N(μ,σ2){displaystyle Ysim {mbox{Log-N}}(mu ,sigma ^{2})}是对数正态分布如果Y=eX{displaystyle Y=e^{X}}并且X∼N(μ,σ2){displaystyle Xsim N(mu ,sigma ^{2})}.


• 与Lévy skew alpha-stable分布相关：如果X∼Levy-SαS(2,β,σ/2,μ){displaystyle Xsim {textrm {Levy-S}}alpha {textrm {S}}(2,beta ,sigma /{sqrt {2}},mu )}因而X∼N(μ,σ2){displaystyle Xsim N(mu ,sigma ^{2})}.

參量估計

參數的極大似然估計

概念一般化

多元正态分布的協方差矩陣的估計的推導是比較難於理解的。它需要瞭解譜原理（spectral theorem）以及為什麼把一個標量看做一個1×1矩阵(matrix)的迹(trace)而不僅僅是一個標量更合理的原因。請參考協方差矩陣的估計（estimation of covariance matrices）.

參數的矩估計

常見實例

光子計數

計量誤差

飲料裝填量不足與超量的機率

某飲料公司裝瓶流程嚴謹，每罐飲料裝填量符合平均600毫升，標準差3毫升的常態分配法則。隨機選取一罐，求（1）容量超過605毫升的機率；（2）容量小於590毫升的機率。

容量超過605毫升的機率 = p ( X > 605)= p ( ((X-μ) /σ) > ( (605 – 600) / 3) )= p ( Z > 5/3) = p( Z > 1.67) = 1 - 0.9525 = 0.0475

容量小於590毫升的機率 = p (X < 590) = p ( ((X-μ) /σ) < ( (590 – 600) / 3) )= p ( Z < -10/3) = p( Z < -3.33) = 0.0004

6-標準差(6-sigma或6-σ)的品質管制標準

6-標準差(6-sigma或6-σ)，是製造業流行的品質管制標準。在這個標準之下，一個標準常態分配的變數值出現在正負三個標準差之外，只有2* 0.0013= 0.0026 (p (Z < -3) = 0.0013以及p(Z > 3) = 0.0013)。也就是說，這種品質管制標準的產品不良率只有萬分之二十六。假設例中的飲料公司裝瓶流程採用這個標準，而每罐飲料裝填量符合平均600毫升，標準差3毫升的常態分配。那么預期裝填容量的範圍應該多少？

6-標準差的範圍 = p ( -3 < Z < 3)= p ( - 3 < (X-μ) /σ < 3) = p ( -3 < (X- 600) / 3 < 3)= p ( -9 < X – 600 < 9) = p (591 < X < 609)
因此，預期裝填容量應該介於591至609毫升之間。

生物標本的物理特性

金融變量

壽命

測試和智力分布

計算學生智商高低的機率

假設某校入學新生的智力測驗平均分數與标准差分別為100與12。那麼隨機抽取50個學生，他們智力測驗平均分數大於105的機率？小於90的機率？

本例沒有常態分配的假設，還好中央極限定理提供一個可行解，那就是當隨機樣本長度超過30，樣本平均數x¯{displaystyle {bar {x}}}近似於一個常態變數，

因此標準常態變數Z=X¯−μσ/n{displaystyle Z={frac {{bar {X}}-mu }{sigma /{sqrt {n}}}}}。

平均分數大於105的機率 P(Z>105−10012/50)=P(Z>5/1.7)=P(Z>2.94)=0.0016{displaystyle P(Z>{frac {105-100}{12/{sqrt {50}}}})=P(Z>5/1.7)=P(Z>2.94)=0.0016}

平均分數小於90的機率 P(Z<90−10012/50)=P(Z<−5.88)=0.0000{displaystyle P(Z<{frac {90-100}{12/{sqrt {50}}}})=P(Z<-5.88)=0.0000}

计算统计应用

生成正态分布随机变量

在计算机模拟中，经常需要生成正态分布的数值。最基本的一个方法是使用标准的正态累积分布函数的反函数。除此之外还有其他更加高效的方法，Box-Muller变换就是其中之一。另一个更加快捷的方法是ziggurat算法。下面将介绍这两种方法。一个简单可行的并且容易编程的方法是：求12个在（0,1）上均匀分布的和，然后减6(12的一半)。这种方法可以用在很多应用中。这12个数的和是Irwin-Hall分布；选择一个方差12。这个随即推导的结果限制在（-6,6）之间，并且密度为12，是用11次多项式估计正态分布。

Box-Muller方法是以两组独立的随机数U和V，这两组数在(0,1]上均匀分布，用U和V生成两组独立的标准常态分布随机变量X和Y:

X=−2ln⁡Ucos⁡(2πV),{displaystyle X={sqrt {-2ln U}},cos(2pi V),}

Y=−2ln⁡Usin⁡(2πV){displaystyle Y={sqrt {-2ln U}},sin(2pi V)}。

这个方程的提出是因为二自由度的卡方分布（见性质4）很容易由指数随机变量（方程中的lnU）生成。因而通过随机变量V可以选择一个均匀环绕圆圈的角度，用指数分布选择半径然后变换成（正态分布的）x,y坐标。

参考文献

• John Aldrich. Earliest Uses of Symbols in Probability and Statistics.網上材料，2006年6月3日存在.(See "Symbols associated with the Normal Distribution".)


• 
  Abraham de Moivre (1738年). The Doctrine of Chances.


• 
  Stephen Jay Gould (1981年). The Mismeasure of Man. First edition. W. W. Norton. ISBN 978-0-393-01489-1.


• 
  R. J. Herrnstein and Charles Murray (1994年). The Bell Curve: Intelligence and Class Structure in American Life. Free Press. ISBN 978-0-02-914673-6.


• 
  Pierre-Simon Laplace (1812年). Analytical Theory of Probabilities.


• Jeff Miller, John Aldrich, et al. Earliest Known Uses of Some of the Words of Mathematics. In particular, the entries for "bell-shaped and bell curve", "normal" (distribution), "Gaussian", and "Error, law of error, theory of errors, etc.".網上材料，2006年6月3日存在


• S. M. Stigler (1999年). Statistics on the Table, chapter 22. Harvard University Press. (History of the term "normal distribution".)


• 
  Eric W. Weisstein et al. Normal Distribution at MathWorld.網上材料，2006年6月3日存在。


• Marvin Zelen and Norman C. Severo (1964年). Probability Functions. Chapter 26 of Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, ed, by Milton Abramowitz and Irene A. Stegun. National Bureau of Standards.

外部链接

维基共享资源中相关的多媒体资源：正态分布

• 
  Interactive Distribution Modeler (incl. Normal Distribution).


• basic tools for sixsigma


• PlanetMath: normal random variable


• GNU Scientific Library – Reference Manual – The Gaussian Distribution


• 
  Distribution Calculator – Calculates probabilities and critical values for normal, t, chi-square and F-distribution.


• Inverse Cumulative Standard Normal Distribution Function


• Public Domain Normal Distribution Table


• Is normal distribution due to Karl Gauss? Euler, his family of gamma functions, and place in history of statistics


• Maxwell demons: Simulating probability distributions with functions of propositional calculus


• Normal distribution table


• 
  The Doctrine of Chance at MathPages.


• 正态分布的前世今生(上)


• 正态分布的前世今生(下)


• 在线计算器 正态分布

參見

• 中心極限定理


• 概率論


• 伽玛分布