偶極子

地球磁場可以近似為一個磁偶極子的磁場。但是,圖內的 N 和 S 符號分別標示地球的地理北極和地理南極。這標示法很容易引起困惑。實際而言,地球的磁偶極矩的方向,是從地球位於地理北極附近的地磁北極,指向位於地理南極附近的地磁南極;而磁偶極子的方向則是從指南極指向指北極。

電極偶子的等值線圖。等值曲面清楚地區分於圖內。
在電磁學裏,有兩種偶極子(dipole):
電偶極子是兩個分隔一段距離,電量相等,正負相反的電荷。
磁偶極子是一圈封閉循環的電流。例如一個有常定電流運行的線圈。
偶極子的性質可以用它的偶極矩描述。
電偶極矩(p{displaystyle mathbf {p} }

除了載流迴路以外,電子和許多基本粒子都擁有磁偶極矩。它們都會產生磁場,與一個非常小的載流迴路產生的磁場完全相同。但是,現時大多數的科學觀點認為這個磁偶極矩是電子的自然性質,而非由載流迴路生成。
永久磁鐵的磁偶極矩來自於電子內稟的磁偶極矩。長條形的永久磁鐵稱為條形磁鐵,其兩端稱為指北極和指南極,其磁偶極矩的方向是由指南極朝向指北極。這常規與地球的磁偶極矩恰巧相反:地球的磁偶極矩的方向是從地球的地磁北極指向地磁南極。地磁北極位於北極附近,實際上是指南極,會吸引磁鐵的指北極;而地磁南極位於南極附近,實際上是指北極,會吸引磁鐵的指南極。羅盤磁針的指北極會指向地磁北極;條形磁鐵可以當作羅盤使用,條形磁鐵的指北極會指向地磁北極。
根據當前的觀察結果,磁偶極子產生的機制只有兩種,載流迴路和量子力學自旋。科學家從未在實驗裏找到任何磁單極子存在的證據。
目录
1 物理偶極子、點偶極子、近似偶極子
2 分子的電偶極矩
3 電偶極子的電場
3.1 導引
4 磁偶極子的磁場
5 作用於偶極極子的力矩
6 偶極輻射
7 量子力學的電偶極子算符
8 參閱
9 參考文獻
10 外部連結
物理偶極子、點偶極子、近似偶極子

分開有限距離的兩個異性電荷的電場線。
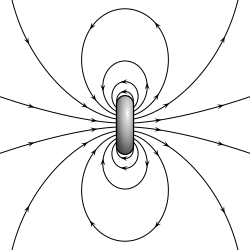
有限直徑的載流迴圈的磁場線。

任意點偶極子(電偶極子、磁偶極子、聲偶極子等等)的場線。
一個物理電偶極子是由兩個等電量的異性點電荷構成的。在距離遠超於兩個點電荷相隔距離之處,物理電偶極子所產生的電場,可以近似為其電偶極矩所產生的電場。令物理電偶極子的兩個點電荷相隔距離趨向於 0 ,同時保持其電偶極矩不變,則極限就是點電偶極子,又稱為純電偶極子。物理電偶極子產生的電場的多極展開式中,一次項目就是點電偶極子產生的電場。物理電偶極子的電偶極矩 p{displaystyle mathbf {p} }
p=qd{displaystyle mathbf {p} =qmathbf {d} };
其中,q{displaystyle q}

到現今為止,雖然還沒有找到任何磁單極子存在的證據,科學家可以在電子和許多基本粒子的物理行為中,找到以量子力學的自旋形式存在的磁偶極子。點磁偶極子所產生的磁場的形態與點電偶極子所產生的電場的形態完全相同。非常小的載流迴路可以近似為點磁偶極子。物理磁偶極子 m{displaystyle mathbf {m} }
m=Ia{displaystyle mathbf {m} =Imathbf {a} };
其中,I{displaystyle I}

任何電荷或電流組態都具有偶極矩,其對應的偶極子所產生的向量場,是那個組態在遠距離的最好近似。偶極子項只是多極展開式中的一項。當單極矩等於 0 時(對磁案例而言,此情况永遠成立,因為磁單極子不存在),在遠距離 r{displaystyle r}





分子的電偶極矩
很多分子都擁有電偶極矩。這是因為正負電荷的不均勻分佈。例如,
- (正價) H-Cl (負價)
擁有永久電偶極矩的分子稱為極化分子。假若一個分子帶有感應電偶極子,則稱此分子被極化。彼得·德拜是最先研究分子的電偶極子的物理化學家。為了紀念他的貢獻,電偶極矩的測量單位被命名為德拜。
分子的電偶極子又分為以下三種(參閱分子間作用力):
永久電偶極子:假若一個分子內的幾個原子的電荷分布不均,電負性差異很大,则電負性較大的原子會吸引電子更接近自己,因而使得所佔據區域變得更具負性;另外電負性較小的原子的區域會變得更具正性。這樣,正、負電荷中心始終不重合,就形成了永久電偶極子。
瞬時電偶極子:有時候,電子會洽巧地比較集中於分子內的某一個區域,這偶發狀況會產生暫時的電偶極子。
感應電偶極子:當施加外電場於一個分子時,感應這外電場的作用,分子內部正常的電子雲形狀會被改變,因而產生電偶極子。其伴隨的電偶極矩等於外電場和極化性的乘積。
常見的化學化合物在氣態的電偶極矩,採用德拜單位:[1]
二氧化碳:0
一氧化碳:0.112
臭氧:0.53
光氣:1.17
水蒸氣:1.85
氰化氫:2.98
氨基氰:4.27
溴化鉀:10.41
這些數值可從相對電容率的測量值計算求得。當分子因為對稱性而使得浄電偶極矩被抵消,則設定電偶極矩為 0 。電偶極矩最大值在 10 到 11 這值域內。知道電偶極矩值,科學家可以推論分子的分子結構。例如,數據顯示出,二氧化碳是一個線性分子;而臭氧則不是。
電偶極子的電場
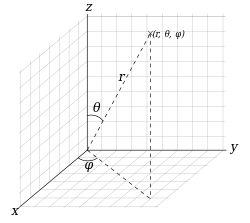
球坐標 (r, θ, ϕ){displaystyle (r, theta , phi )}
 與直角坐標 (x, y, z){displaystyle (x, y, z)}
與直角坐標 (x, y, z){displaystyle (x, y, z)} 之間的關係。
之間的關係。假設電偶極子 p{displaystyle mathbf {p} }



Φ(r)=14πϵ0p⋅r^r2{displaystyle Phi (mathbf {r} )={frac {1}{4pi epsilon _{0}}},{frac {mathbf {p} cdot {hat {mathbf {r} }}}{r^{2}}}};
其中,ϵ0{displaystyle epsilon _{0}}
這公式的右手邊項目是任意靜電勢多極展開式的第二個項目。假若這任意靜電勢是由純電偶極子產生,則這項目是多極展開式的唯一不消失項目。
電偶極子 p{displaystyle mathbf {p} }

E=−∇Φ=14πϵ0r3(3(p⋅r^)r^−p)=p4πϵ0r3(2cosθr^+sinθθ^){displaystyle {begin{aligned}mathbf {E} =-nabla Phi &={frac {1}{4pi epsilon _{0}r^{3}}}left(3(mathbf {p} cdot {hat {mathbf {r} }}){hat {mathbf {r} }}-mathbf {p} right)\&={frac {p}{4pi epsilon _{0}r^{3}}}(2cos theta {hat {mathbf {r} }}+sin theta {hat {boldsymbol {theta }}})end{aligned}}};
其中,θ{displaystyle theta }


注意到這個方程式並不完全正確,這是因為電偶極子的電勢有一個奇點在它所處的位置(原點 O{displaystyle mathbf {O} }
E=−∇Φ=14πϵ0r3(3(p⋅r^)r^−p)−p3ϵ0δ3(r)=p4πϵ0r3(2cosθr^+sinθθ^)−p3ϵ0δ3(r){displaystyle {begin{aligned}mathbf {E} =-nabla Phi &={frac {1}{4pi epsilon _{0}r^{3}}}left(3(mathbf {p} cdot {hat {mathbf {r} }}){hat {mathbf {r} }}-mathbf {p} right)-{frac {mathbf {p} }{3epsilon _{0}}}delta ^{3}(mathbf {r} )\&={frac {p}{4pi epsilon _{0}r^{3}}}(2cos theta {hat {mathbf {r} }}+sin theta {hat {boldsymbol {theta }}})-{frac {mathbf {p} }{3epsilon _{0}}}delta ^{3}(mathbf {r} )end{aligned}}};
其中,δ3(r){displaystyle delta ^{3}(mathbf {r} )}
導引
從計算電偶極子所產生的電場的平均值,可以得到正確答案。設定以原點 O{displaystyle mathbf {O} }


⟨E⟩=34πb3∫VEd3r=34πb3∫0b∫02π∫0πp4πϵ0r3(2cosθr^+sinθθ^)r2sinθ dθdϕdr{displaystyle langle mathbf {E} rangle ={frac {3}{4pi b^{3}}}int _{mathbb {V} }mathbf {E} mathrm {d} ^{3}mathbf {r} ={frac {3}{4pi b^{3}}}int _{0}^{b}int _{0}^{2pi }int _{0}^{pi }{frac {p}{4pi epsilon _{0}r^{3}}}(2cos theta {hat {mathbf {r} }}+sin theta {hat {boldsymbol {theta }}})r^{2}sin theta mathrm {d} theta mathrm {d} phi mathrm {d} r}。
注意到球坐標單位向量與直角坐標單位向量之間的關係:
r^=x^sinθcosϕ+y^sinθsinϕ+z^cosθ{displaystyle {hat {mathbf {r} }}={hat {mathbf {x} }}sin theta cos phi +{hat {mathbf {y} }}sin theta sin phi +{hat {mathbf {z} }}cos theta }、
θ^=x^cosθcosϕ+y^cosθsinϕ−z^sinθ{displaystyle {hat {boldsymbol {theta }}}={hat {mathbf {x} }}cos theta cos phi +{hat {mathbf {y} }}cos theta sin phi -{hat {mathbf {z} }}sin theta }。
將這兩個關係式代入前面積分式,可以得到
⟨E⟩{displaystyle langle mathbf {E} rangle }
=3p16π2ϵ0b3∫0b∫02π∫0π1r3{displaystyle ={frac {3p}{16pi ^{2}epsilon _{0}b^{3}}}int _{0}^{b}int _{0}^{2pi }int _{0}^{pi }{frac {1}{r^{3}}}}
[3sinθcosθcosϕx^{displaystyle [3sin theta cos theta cos phi {hat {mathbf {x} }}}
+3sinθcosθsinϕy^{displaystyle +3sin theta cos theta sin phi {hat {mathbf {y} }}}
+(2cos2θ−sin2θ)z^]{displaystyle +(2cos ^{2}theta -sin ^{2}theta ){hat {mathbf {z} }}]}
r2sinθ dθdϕdr{displaystyle r^{2}sin theta mathrm {d} theta mathrm {d} phi mathrm {d} r}。
注意到這積分式的x-分量與y-分量都等於零,只剩下z-分量:
⟨E⟩=3p16π2ϵ0b3∫0b∫02π∫0π1r(2cos2θ−sin2θ)z^sinθ dθdϕdr=3pz^8πϵ0b3∫0b1r dr∫0π(2sinθcos2θ−sin3θ) dθ{displaystyle {begin{aligned}langle mathbf {E} rangle &={frac {3p}{16pi ^{2}epsilon _{0}b^{3}}}int _{0}^{b}int _{0}^{2pi }int _{0}^{pi }{frac {1}{r}}(2cos ^{2}theta -sin ^{2}theta ){hat {mathbf {z} }}sin theta mathrm {d} theta mathrm {d} phi mathrm {d} r\&={frac {3p{hat {mathbf {z} }}}{8pi epsilon _{0}b^{3}}}int _{0}^{b}{frac {1}{r}} mathrm {d} rint _{0}^{pi }(2sin theta cos ^{2}theta -sin ^{3}theta ) mathrm {d} theta end{aligned}}}。
對於徑向坐標 r{displaystyle r}
∫0b1r dr=−∞{displaystyle int _{0}^{b}{frac {1}{r}} mathrm {d} r=-infty }!
但對於天頂角 θ{displaystyle theta }
∫0π(2sinθcos2θ−sin3θ) dθ=∫0π(2sinθcos2θ−sin3θ) dθ=0{displaystyle int _{0}^{pi }(2sin theta cos ^{2}theta -sin ^{3}theta ) mathrm {d} theta =int _{0}^{pi }(2sin theta cos ^{2}theta -sin ^{3}theta ) mathrm {d} theta =0}!
由此可知,從這運算無法得到 ⟨E⟩{displaystyle langle mathbf {E} rangle }



⟨E⟩=34πb3∫VE d3r=− 34πb3∫V∇ϕ d3r=− 34πb3∮Sϕ dS{displaystyle langle mathbf {E} rangle ={frac {3}{4pi b^{3}}}int _{mathbb {V} }mathbf {E} mathrm {d} ^{3}mathbf {r} =- {frac {3}{4pi b^{3}}}int _{mathbb {V} }nabla phi mathrm {d} ^{3}mathbf {r} =- {frac {3}{4pi b^{3}}}oint _{mathbb {S} }phi mathrm {d} mathbf {S} };
其中,S{displaystyle mathbb {S} }

將電勢 ϕ{displaystyle phi }

⟨E⟩=− 3(4π)2bϵ0∮S[∫V′ρ(r′)|br^−r′| d3r′]r^ sinθ dθdϕ{displaystyle langle mathbf {E} rangle =- {frac {3}{(4pi )^{2}bepsilon _{0}}}oint _{mathbb {S} }left[int _{mathbb {V} '}{frac {rho (mathbf {r} ')}{|b{hat {mathbf {r} }}-mathbf {r} '|}} mathrm {d} ^{3}mathbf {r} 'right]{hat {mathbf {r} }} sin theta mathrm {d} theta mathrm {d} phi };
其中,ρ(r′){displaystyle rho (mathbf {r} ')}





場位置與源位置之間距離的倒數以球諧函數 Yℓm(θ,ϕ){displaystyle Y_{ell m}(theta ,phi )}
1|br^−r′|=∑ℓ=0∞∑m=−ℓℓ4π2ℓ+1r′ℓbℓ+1Yℓm∗(θ′,ϕ′)Yℓm(θ,ϕ),r′<b{displaystyle {frac {1}{|b{hat {mathbf {r} }}-mathbf {r} '|}}=sum _{ell =0}^{infty }sum _{m=-ell }^{ell }{frac {4pi }{2ell +1}}{frac {r^{prime ell }}{b^{ell +1}}}Y_{ell m}^{*}(theta ',phi ')Y_{ell m}(theta ,phi ),qquad r'<b};
其中,br^{displaystyle b{hat {mathbf {r} }}}



單位向量 r^{displaystyle {hat {mathbf {r} }}}
r^=x^sinθcosϕ+y^sinθsinϕ+z^cosθ=x^[−2π3(−Y1,−1∗+Y11∗)]+y^[−2π3(−Y1,−1∗−Y11∗)]+z^4π3Y10∗{displaystyle {begin{aligned}{hat {mathbf {r} }}&={hat {mathbf {x} }}sin theta cos phi +{hat {mathbf {y} }}sin theta sin phi +{hat {mathbf {z} }}cos theta \&={hat {mathbf {x} }}left[-{sqrt {frac {2pi }{3}}}(-Y_{1,-1}^{*}+Y_{11}^{*})right]+{hat {mathbf {y} }}left[-{sqrt {frac {2pi }{3}}}(-Y_{1,-1}^{*}-Y_{11}^{*})right]+{hat {mathbf {z} }}{sqrt {frac {4pi }{3}}}Y_{10}^{*}\end{aligned}}}。
應用球諧函數的正交歸一性
∫02π∫0πYℓ′m′∗(θ,ϕ)Yℓm(θ,ϕ)sinθ dθdϕ=δℓℓ′δmm′{displaystyle int _{0}^{2pi }int _{0}^{pi }Y_{ell 'm'}^{*}(theta ,phi )Y_{ell m}(theta ,phi )sin theta mathrm {d} theta mathrm {d} phi =delta _{ell ell '}delta _{mm'}},
可以得到 ⟨E⟩{displaystyle langle mathbf {E} rangle }

⟨E⟩=− 14πb3ϵ0∫V′r′ρ(r′) d3r′=− p4πb3ϵ0{displaystyle langle mathbf {E} rangle =- {frac {1}{4pi b^{3}epsilon _{0}}}int _{mathbb {V} '}mathbf {r} 'rho (mathbf {r} ') mathrm {d} ^{3}mathbf {r} '=- {frac {mathbf {p} }{4pi b^{3}epsilon _{0}}}}。
也就是說,
∫VE d3r=− p3ϵ0{displaystyle int _{mathbb {V} }mathbf {E} mathrm {d} ^{3}mathbf {r} =- {frac {mathbf {p} }{3epsilon _{0}}}}。
為了滿足這性質,必需對於電偶極子 p{displaystyle mathbf {p} }

E=14πϵ0r3(3(p⋅r^)r^−p)−p3ϵ0δ3(r)=p4πϵ0r3(2cosθr^+sinθθ^)−p3ϵ0δ3(r){displaystyle {begin{aligned}mathbf {E} &={frac {1}{4pi epsilon _{0}r^{3}}}left(3(mathbf {p} cdot {hat {mathbf {r} }}){hat {mathbf {r} }}-mathbf {p} right)-{frac {mathbf {p} }{3epsilon _{0}}}delta ^{3}(mathbf {r} )\&={frac {p}{4pi epsilon _{0}r^{3}}}(2cos theta {hat {mathbf {r} }}+sin theta {hat {boldsymbol {theta }}})-{frac {mathbf {p} }{3epsilon _{0}}}delta ^{3}(mathbf {r} )end{aligned}}}。
這樣,在計算 ⟨E⟩{displaystyle langle mathbf {E} rangle }
磁偶極子的磁場
假設磁偶極矩為 m{displaystyle mathbf {m} }


A(r)=μ04πr2(m×r^){displaystyle mathbf {A} (mathbf {r} )={frac {mu _{0}}{4pi r^{2}}}(mathbf {m} times {hat {mathbf {r} }})};
其中,μ0{displaystyle mu _{0}}
這磁偶極子所產生的磁場 B{displaystyle mathbf {B} }
B=∇×A{displaystyle mathbf {B} =nabla times mathbf {A} }。
由於磁偶極子的向量勢有一個奇點在它所處的位置(原點 O{displaystyle mathbf {O} }
B(r)=μ04πr3(3(m⋅r^)r^−m)+2μ0m3δ3(r){displaystyle mathbf {B} (mathbf {r} )={frac {mu _{0}}{4pi r^{3}}}left(3(mathbf {m} cdot {hat {mathbf {r} }}){hat {mathbf {r} }}-mathbf {m} right)+{frac {2mu _{0}mathbf {m} }{3}}delta ^{3}(mathbf {r} )}。
任意磁場的多極展開式中,帶頭項目就是這公式右手邊的第一個項目,偶極子項目。磁場沒有單極子項目。在遠距離,這公式近似任何類似磁偶極子的組態所產生的磁場。
偶極磁場的狄拉克δ函數項目造成了原子能級分裂,因而形成了超精細結構(hyperfine structure)[3]。在天文學裏,氫原子的超精細結構給出了21公分譜線,在電磁輻射的無線電波範圍,是除了3K背景輻射以外,宇宙彌漫最廣闊的電磁輻射。從復合紀元(recombination)至再電離紀元(reionization)之間的天文學研究,只能依靠觀測21公分譜線無線電波。
作用於偶極極子的力矩
將一磁偶極子放在均勻磁場,或將電偶極子放在均勻電場,偶極子的兩端會分別各產生一個力,兩個大小相等而方向相反的力產生力矩 τ{displaystyle {boldsymbol {tau }}}
τ=p×E{displaystyle {boldsymbol {tau }}=mathbf {p} times mathbf {E} }、
τ=m×B{displaystyle {boldsymbol {tau }}=mathbf {m} times mathbf {B} }。
力矩傾向將偶極子的方向與向量場的方向排向同一方向,偶極子的位能是
U=−p⋅E{displaystyle U=-mathbf {p} cdot mathbf {E} }、
U=−m⋅B{displaystyle U=-mathbf {m} cdot mathbf {B} }。
在計算時,我們常假設偶極子兩端之間的距離是無窮小,即點偶極子。
偶極輻射

一個震盪電偶極子的電場的即時演化。
在靜電學和靜磁學之外,很重要的物理領域是含時偶極子。
當一個電偶極子在做諧振蕩時,其電偶極矩可以表示為 p=p′(r)e−iωt{displaystyle mathbf {p} =mathbf {p'(mathbf {r} )} e^{-iomega t}}

E=14πε0{ω2c2rr^×p×r^+(1r3−iωcr2)[3r^(r^⋅p)−p]}eiωr/c{displaystyle mathbf {E} ={frac {1}{4pi varepsilon _{0}}}left{{frac {omega ^{2}}{c^{2}r}}{hat {mathbf {r} }}times mathbf {p} times {hat {mathbf {r} }}+left({frac {1}{r^{3}}}-{frac {iomega }{cr^{2}}}right)left[3{hat {mathbf {r} }}({hat {mathbf {r} }}cdot mathbf {p} )-mathbf {p} right]right}e^{iomega r/c}}、
B=ω24πε0c3r^×p(1−ciωr)eiωr/cr{displaystyle mathbf {B} ={frac {omega ^{2}}{4pi varepsilon _{0}c^{3}}}{hat {mathbf {r} }}times mathbf {p} left(1-{frac {c}{iomega r}}right){frac {e^{iomega r/c}}{r}}}。
在離開偶極子很遠的位置(rω/c≫1{displaystyle romega /cgg 1}
B=ω24πε0c3(r^×p)eiωr/cr{displaystyle mathbf {B} ={frac {omega ^{2}}{4pi varepsilon _{0}c^{3}}}({hat {mathbf {r} }}times mathbf {p} ){frac {e^{iomega r/c}}{r}}}、
E=cB×r^{displaystyle mathbf {E} =cmathbf {B} times {hat {mathbf {r} }}}。
經過時間平均,產生的總輻射功率 P{displaystyle P}
P=ω412πε0c3|p|2{displaystyle P={frac {omega ^{4}}{12pi varepsilon _{0}c^{3}}}|mathbf {p} |^{2}}。
功率的分佈並不具有均向性,而是集中於垂直於電偶極矩的方向。
量子力學的電偶極子算符
試想一群粒子,數量為 N{displaystyle N}








p=∑i=1Nqiri{displaystyle {mathfrak {p}}=sum _{i=1}^{N},q_{i},mathbf {r} _{i}}。
參閱
- 電介質
- 永電體
印度洋電偶極子(Indian Ocean Dipole)
自旋磁矩(spin magnetic moment)
軸多極矩(Axial multipole moments)- 圓柱多極矩
- 球多極矩
拉普拉斯展開式(位勢論)(Laplace expansion (potential))- 勒讓德多項式
參考文獻
^ Weast, Robert C. CRC Handbook of Chemistry and Physics 65rd ed. CRC Press. 1984. ISBN 0-8493-0465-2. 引文格式1维护:冗余文本 (link)
^ 2.02.1 Jackson, John David, Classical Electrodynamic 3rd., USA: John Wiley & Sons, Inc.: pp. 107–111145–150, 184–188, 1999, ISBN 978-0-471-30932-1 引文格式1维护:冗余文本 (link)
^ Griffiths, David J., Hyperfine splitting in the ground state of hydrogen (PDF), American Journal of Physics, August 1982, 50 (8): pp. 698 引文格式1维护:冗余文本 (link)
外部連結
波士頓大學物理模擬示範網頁: 電偶極子的電場線圖和電場向量圖



![+(2cos ^{2}theta -sin ^{2}theta ){hat {{mathbf {z}}}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7b67066bf3f622ce44567db4223f320d8d55386)