异或门
基本逻辑门 | |
| BUF | NOT |
| AND | NAND |
| OR | NOR |
| XOR | XNOR |
| IMP | NIMP |
输入 A B | 输出 A XOR B | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
异或门(英语:Exclusive-OR gate,簡稱XOR gate,又稱EOR gate、ExOR gate)是数字逻辑中实现逻辑异或的逻辑门,功能见右侧真值表。若两个输入的电平相异,则输出为高电平(1);若两个输入的电平相同,则输出为低电平(0)。
这一函数能实现模为2的加法,因此,异或门可以实现计算机中的二进制加法。半加器是由异或门和与门组成的。
目录
1 概述
2 硬件描述和引脚分配
3 传输门连线
4 备选方案
5 2个输入以上的情况
6 其他应用
6.1 加法器
6.2 异或密码
6.3 异或校验
6.4 异或门倍频器
6.5 可控反相器
7 参见
8 参考文献
概述
下列包括逻辑门的3种符号:形状特征型符号(ANSI/IEEE Std 91-1984)、IEC矩形国标符号(IEC 60617-12)和不再使用的DIN符号(DIN 40700)。其他的逻辑门符号见逻辑门符号表。
| 表达式 | 符号 | 功能表 | 继电器逻辑 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ANSI/IEEE Std 91-1984 | IEC 60617-12 | DIN 40700 | ||||||||||||||||||
Y=A⊕B{displaystyle Y=Aoplus B}  Y=A∨_B{displaystyle Y=A,{underline {lor }},B}  |  | 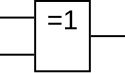 | 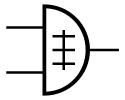 或  |
|  | |||||||||||||||
Y=A⊕B{displaystyle Y=Aoplus B}

异或的运算顺序如下:
- (w∨_x∨_y∨_z)⇔(((w∨_x)∨_y)∨_z){displaystyle left(w,{underline {lor }},x,{underline {lor }},y,{underline {lor }},zright)Leftrightarrow left(left(left(w,{underline {lor }},xright),{underline {lor }},yright),{underline {lor }},zright)}
输入的顺序对输出没有影响,因为异或满足结合律。
与非逻辑实现的异或运算的逻辑表达式如下:
- x∨_y⇔(x∧¯(x∧¯y))∧¯(y∧¯(x∧¯y)){displaystyle x,{underline {lor }},yLeftrightarrow left(x,{overline {land }},left(x,{overline {land }},yright)right),{overline {land }},left(y,{overline {land }},left(x,{overline {land }},yright)right)}
硬件描述和引脚分配
异或门是基本的逻辑门,因此在TTL和CMOS集成电路中都是可以使用的。标准的4000系列CMOS集成电路为4070,包含四个独立的2输入异或门。4070替换了可靠性差的4030,但二者的引脚分配相同。下面是引脚分配表:
 4070四异或门DIP封装集成电路的引脚分配图 | .mw-parser-output .templatequote{margin-top:0;overflow:hidden}.mw-parser-output .templatequote .templatequotecite{line-height:1em;text-align:left;padding-left:2em;margin-top:0}.mw-parser-output .templatequote .templatequotecite cite{font-size:small}
|
包括NXP在内的很多半导体制造商都生产这一元件,封装方式分为直插DIP封装和SOIC封装两种。元件的数据表可在大多数元件数据库查询到。
传输门连线
异或门可以用MOSFET组成。下图是CMOS实现的异或门。[1]
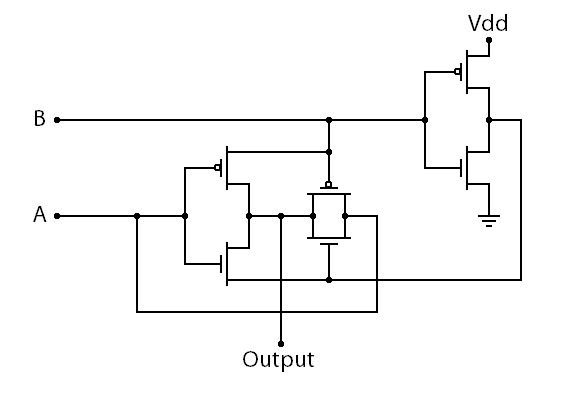
异或门的传输门连线
备选方案

CMOS异或门

利用 NOT, AND, OR 組成的異或門
輸入1和1時,XOR會輸出0。因此,不可能只使用AND和OR組成XOR,必須包含反相器(NOT)。
如果没有特定的逻辑门,我们可以用其他现有的逻辑门构建。显而易见的一个方法是用同或门後接一个非门来实现异或门。如果按照逻辑表达式A⋅B¯+A¯⋅B{displaystyle Acdot {overline {B}}+{overline {A}}cdot B}
异或门可利用四个与非门或五个或非门来实现,连线方法见下图。因为与非门和或非门是“通用的门电路”,因此任何一个逻辑函数都可单独由与非逻辑或或非逻辑来实现。
 仅用与非门(NAND)实现的异或门 |  仅用或非门(NOR)实现的异或门 |
留意下表,OR和NAND中間兩行輸出跟XOR相同,第一和第四行不同。所以,利用OR和NAND再加上AND可以組成XOR。
| A | B | OR | NAND | XOR |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
2个输入以上的情况
若严格的理解逻辑异或的定义,或观察IEC符号,我们就会提出关於2输入以上的异或门是否能有正确表现的问题。如果一个逻辑门能有3个或更多的输入,并能得到正确的输出,而且输入中的一个为真,那么这个逻辑门在效果上是一个单热检测器,而其实这是仅有2个输入的情况。不过,实际中极少用这种方法来实现这一装置。
将连续相接的输入接入级联的异或门是很常见的连接方式。首先将2个信号作为一个异或门的输入,然後将其输出以及第3个信号作为第二个异或门的输入,对需要接入的其他信号反复进行以上操作,这样就会得到如下结果:若输入中高电平(1)的个数是奇数,输出为高电平(1);若输入中高电平(1)的个数是偶数,输出为低电平(0)。这种特性在实际应用中可实现奇偶发生器或模2加法器。
例如,74LVC1G386微型集成电路是3输入异或门,可实现奇偶发生器[2]。
Verilog的缩减运算符能将任意位输入进行从高位到低位逐次异或运算,得到一位输出。
其他应用
加法器

异或门可以作为一位加法器,可将任何2位相加得到1个输出。若两个输入的值均为1,则得到10的结果,而与门由两个输入的值控制进位的输出。以上是半加器的主要原理。
异或密码
安全加密算法一次性密碼本就是利用异或门实现的。加密的原理是将要加密的文件(明文)编码成二进制序列,然後将与被加密的消息长度相同的随机二进制序列作为密钥,再将明文与密钥的每一位依次进行按位异或运算,得到密文。若将密文与密钥的每一位依次进行按位异或运算,就能得到原文。
异或校验
| 101 XOR 011 = 110 |
| 110 XOR 011 = 101 |
| 110 XOR 101 = 011 |
将两个3位二进制序列101和011进行异或奇偶校验可得到异或校验和110(右表第一行右侧)。若序列101丢失,我们可以将已知序列011与异或校验和进行异或运算得到丢失的序列(右表第二行)。
异或门倍频器

数字信号倍频器
将方波信号和利用RC電路延迟的方波信号作为异或门的两个输入,可以很容易的得到频率达到100 MHz以上的方波。输出得到的针尖脉冲是锁相的,其频率会与RC电路的时间常数基本保持同步。由於这种倍频器不需要共振濾波器,输入信号可以具有经过调频的任意占空比,也可以是强信号。
可控反相器
将异或门的一个输入作为信号输入端,另一个输入作为控制端,若控制端为低电平(0),信号输出不变;若控制端为高电平(1),异或门表现为反相器,信号输出反相。
参见
维基共享资源中相关的多媒体资源:异或门 |
- 逻辑异或
- 同或门
- 逻辑代数
- 逻辑门
参考文献
^ Paul Falstad's Circuit Simulator Applet
^ 74LVC1G386 互联网档案馆的存檔,存档日期2009-12-29.数据表
Tietze, Ulrich; Schenk, Christoph. Halbleiter-Schaltungstechnik. Springer. 2002年12月. ISBN 3-540-42849-6.
Beuth, Klaus. Digitaltechnik. Vogel. 1998年10月. ISBN 3-8023-1755-6.
Seifart, Manfred; Beikirch, Helmut. Digitaltechnik. Technik. 1998年5月. ISBN 3-341-01198-6.
| ||||||||||||||
| ||||||||||||||||||||||||















