日晷
| 本條目部分链接不符合格式手冊規範。跨語言链接及章節標題等處的链接可能需要清理。 (2015年12月11日) |

這個日晷位於澳大利亞的墨爾本。晷影器是三角形的葉片,其傾斜的邊緣是晷針。

在英格蘭薩福克郡奧爾德伯勒,在議論大廳面向南南西的垂直日晷。

一對母女在希臘雅典的國家公園觀看一個安裝在那兒的日晷。

香港科技大學的地標──位於廣場正中央的日晷
日晷是一種由視太陽位置告知每天時間的裝置。狹義而言,它包含一個平面(盤面)和將影子投影在平面上以指示時間的晷影器(gnomon)組成。當太陽移動著劃過天際,陰影邊緣會與不同的時間線對齊,顯示出當時的時刻。晷針(style)就是在晷影器上指示時間的邊緣線;經由晷針上的節點(如果有),還可以提示日期。晷影器可以產生明顯的陰影,以讓晷針可以顯示時間。晷影器可以是一根棍棒、金屬線、或精心裝飾的雕飾。晷針必須平行於地球的自轉軸,才能整年都提供正確的時間。晷針與地平面的夾角就是其所在位置的地理緯度。
廣義而言,日晷是使用太陽的高度或方位(或兩者一起)以顯示時間的任何設備。除了提供時間的功能外,日晷也常被當成裝置藝術的一部分、文學上的隱喻和數學上學習的物件。
一般常見廉價的裝飾日晷是大批量產的,所以晷針的角度與時角是不正確的,也就不能提供正確的時間[1]。
目录
1 簡介
2 太陽的視運動
3 歷史
3.1 中國
3.2 歷史古跡
4 專門名詞
5 在南半球的日晷
6 從日晷讀取時間的調整和鐘錶時間的計算
6.1 夏令時間(日光節約時間)的調整
6.2 時區(經度)修正
6.3 均時差的修正
7 日晷的標準設施
8 晷影器軸固定的日晷
8.1 經驗值的時間線標記
8.2 赤道日晷
8.3 水平日晷
8.4 垂直日晷
8.5 口袋日晷
8.6 極日晷
8.7 垂直斜向日晷
8.8 斜倚日晷
8.9 Declining-reclining dials/ Declining-inclining dials
8.9.1 經驗法
8.10 球面日晷
8.11 圓柱形、圓錐形、和其它非平面的日晷
9 變心日晷(Movable-gnomon sundials)
9.1 通用赤道環形日晷
9.2 正投影日晷
9.3 朗伯日晷
10 以高度為準的日晷
10.1 人影日晷
10.2 牧羊人日晷 - 時間棍
10.3 環日晷(Ring dials)
10.4 卡片日晷(斗篷日晷)
11 以節點為基礎的日晷
11.1 摺疊式日晷
11.2 18世紀早期的攜帶式日晷
11.3 等高儀日晷(Elevation sundial)
12 精密日晷 (日光天文鐘)
12.1 赤道弓形日晷
12.2 古希臘的日晷
12.3 地球儀式日晷
12.4 反射日晷
12.5 地平式日晷
13 數位日晷
14 註解
15 參考文獻
16 外部連結
17 参见
簡介
日晷有許多不同的樣式。有些使用陰影或陰影的邊緣,而有些利用線或光點來顯示時間。
產生陰影的物件,稱為晷影器。它可能是細長的桿或其它有明尖銳或直邊的任何物件。一個日晷可能有許多類型的晷影器,這些晷影器可以是固定的,也可以是隨著季節移動的。日晷平面的方向可能垂直、水平與對齊地球的自轉軸,或經由數學的計算而指向任何的方向。[來源請求]
鑒於日晷是使用陽光來指示時間,因此讓陽光透過薄薄的狹縫或通過圓柱透鏡聚焦形成光束,或讓陽光經過一個小孔或一個小圓鏡的反射形成光點,也能用來指示時間。[來源請求]
日晷還可能使用許多類型的表面接收光或陰影。 平面是最常見的表面,但是部分的球面、圓柱、錐面和其它的形狀,也可以使用以增加美觀或精確性。[來源請求]
日晷在其可攜性和指向上也有不同的需求。許多日晷的刻度盤的安裝需要知道當地的緯度、精確的垂直方向(例如,通過水準儀或鉛錘),和真北的方向。可攜式日晷的盤面是可調式的:它可以有兩個不同規則製作的刻度盤,向是一個水平的刻度盤和正投影的刻度盤,一起裝在盤面上。在這些設計中,只有正確放置時,兩個刻度盤才會指示相同的時間,顯示的也才是正確的時間。[來源請求]
除非進行一些修正,日晷顯示的是當地的太陽時。要獲得正確的時鐘時間,需要進行三種類型的更正。
首先,地球的軌道不是理想的圓,自轉的軸也沒有垂直於它的軌道平面,因此日晷顯示的太陽時與鐘錶時在一年中的每一天都會有些許不同的差異,其最大值可以達到15分鐘,這種差別稱為均時差。一個複雜的日晷,可以彎曲它的晷針或時間線來納入這樣的修正。但是日晷通常都是很簡單的,使用一小片說明板或均時差表給出一年中不同日期的修正量。
其次,太陽時必須修正日晷所在地的經度相對於官方時間所在時區經度上的差別。例如,在英國格林威治西方,使用同一個時區時間的日晷,顯示的時間會比官方的時間早。它會在官方時間的正午過後,才會因為太陽稍晚些通過子午線而顯示正午的時間。這種修正往往可以經由旋轉經度上相差的角度來加以修正。
最後,如果還要調整日光節約時間,日晷需要將太陽時調整一個定量的時間,通常是一小時。這種調整通常是使用說明版,或是標示兩組時間來做修正。 [來源請求]
太陽的視運動

一個赤道日晷的頂視圖。小時線在圓上是等分的。同樣的,晷影器(細圓柱棒)的影子也是均勻的移動;晷影器的長度是圓盤外圈半徑的5/12。此動畫模擬的是在夏至日的上午3點至下午9點(不修正日光節約時間),當時太陽的位置在赤緯的最大值(大約23.5°)。當天,在北緯57.05° ,大致是蘇格蘭亞伯丁或阿拉斯加矽地卡的地理緯度,日出和日落時間大約是上午3點和下午9點。
從太陽的視運動最容易理解日晷的原理[2]。地球在它的軸上自轉,並以橢圓軌道繞著太陽公轉。假設太陽是在天球上穩定的圍繞著地球的天體,每24小時繞著天球的軸轉一圈,是一個良好的近似。天球的軸是連接兩個天極之間的直線。由於天球的軸和地球的自轉軸是對齊的,所以當地的水平面與軸的夾角就是地理緯度。
與恆星不同的是,太陽會改變它在天球上的位置。在春天和夏天,它的赤緯度數是正值(在北天球);秋天和冬天,赤緯值是負的,並且有赤緯數值是零的時候(即位於天球赤道時的春分和秋分)。太陽的赤經也會改變,每年在天球上環繞一圈。太陽在天球上經過的路徑稱為黃道,黃道在天球上經過的星座被等分為12個區域,稱為黃道12宮,太陽每年依序經過這12個區域。

在新加坡植物園的日晷。事實上,這個日晷的設計反映出新加坡幾乎位於赤道上。
太陽運動的模型有助於了解日晷。如果投射影子的晷針對準了天極,這是最常見的設計,它的影子會以穩定的速度移動,並且這種旋轉不會隨著季節改變。在這種情況下,全年都可以使用相同的時間線。如果接收陰影的表面垂直於晷針(如赤道日晷)或環繞著晷針(如環形日晷),時間線會是等距劃分。
在其它情況下,即使陰影是均勻的移動,時間線的分配仍會是不均勻的。如果晷針沒有對正天極,或是它的陰影是不均勻的移動,轉動和時間線必須作相對應的修正。光線若是掠過晷針上的一個尖梢,或從鏡子反射,或是穿過一個小孔,就必須依據天極來追蹤影錐。相對應的光點或指標如果落在一個平坦的平面上,將描繪出如同雙曲線、橢圓或圓(在北極或南極點)的圓錐曲線。
這條圓錐曲線是光的影錐與平面相交的截點組成的線。影錐和圓錐曲線會隨著季節變化而改變,也就是隨著太陽的赤緯變化而改變;因此,跟隨著光點位置的反射或陰影位置顯示的日晷,其時間線會有週年性的不同變化。這些都會在牧羊人日晷盤、戒指日晷和方尖石的垂直日晷盤面上呈現出來。另類的日晷,可以改變晷影器相對於時間線的位置或角度(或兩者都改變),例如正投影日晷或朗伯日晷。
歷史

世界上最早的日晷來自埃及的帝王谷(大約西元前1,500年)。
在古老的埃及就有日晷的存在,且其它文化古國,包括中國、希臘和羅馬都存在使用日晷的史料。
從考古紀錄上所知,最古老的日晷是古埃及天文學的方尖碑(西元前3,500年)和巴比倫天文學的影鐘(西元前1,500年)。據推測,人類在更早的日期就已經知道陰影的長度可以量度時間,但很難得到驗證。大約在西元前700年,舊約描述了一個日晷-在大先知書的以賽亞書38:8和歷史書的列王紀20:11提到亞哈謝的日晷。羅馬作家Marcus Vitruvius Pollio(西元前25年)列出了當時所知的日晷和影鐘。修道會日晷是一種規範宗教禮拜時間的日晷。這種日晷從7世紀至14世紀被宗教社群的成員使用著。義大利天文學家帕多伐尼在1570年發表一篇日晷的論文,其中包括製造和勾勒出鋪設壁畫(垂直)和水平日晷的說明。朱塞佩·比安卡尼的Constructio instrumenti ad horologia solaria(約1620年)就在探討如何製作一個完美的日晷。從16世紀以後,它們被廣泛的使用。
中國
中國早在古代就將一根標準高度為八尺的竿子垂直豎立在水平的地面上,在一天裏從早到晚觀察竿子投影的變化,就可以用來計量白天的時間。東漢許慎《說文解字》云:晷,日景也。此處日景即日影。
歷史古跡
- 1985年10月10日-考古學家們在美國伊利諾州西南部的一條河谷中修復了一座巨大的古代印第安人日晷。這個直徑136米的圓圈是由40棵6米高的杉樹幹圍成的,據考證,西元900-1100年間居住在這一帶的克赫克雅印第安人就是用它來分辨四季,確定日期的。
專門名詞

倫敦式地平日晷。晷影器的西側邊緣是正午前用的晷針,之後使用東側的邊緣做晷針。轉換時造成的時間尺度不連續,以正午間隙來跨越與銜接。
一般情況下,日晷是以陰影或光束投擲在稱為晷面或晷盤的表面上來顯示時間。通常是在一個平面上,但也可能是在一個球面、圓柱面、角錐面、螺旋結構和其他各種形狀的內部或外部的表面。[來源請求]
晷盤的表面通常會刻畫上小時線,以顯示陰影或光線落在晷盤上的時間。這些線通常是直線,但也有可能是彎曲的,完全看日晷是如何的設計(見下文)。在有些設計中,可能可以測定一年中的日期,或可能需要知道日期才能得到正確的時間。在這些情況下,可能有多組時間線分別用在不同的月份,或可能設置/計算月份的機制。除了時間線,晷面可能還會提供其他的資料--如地平圈、赤道和回歸線--這些統稱為盤面工具。
製造陰影或光,以投射在晷盤的整個部分稱為日晷的晷影器(gnomon)[3]。然而,晷影器有用的部分通常只是產生陰影的邊緣(或一段線性的特徵),以其所投下來的陰影以確定時間;這段線性的邊緣才是日晷真正的晷針(style)。這個晷針是校準得與天球的軸平行並指向天球極點,因此會與當地的地理子午線一致。在某些日晷的設計上,晷針只是在晷影器邊緣的一個點狀特徵,像是晷針上的一個點狀物,用於確定日期和時間;這個點狀的特徵被稱為日晷的節點(nodus)[3][a]。有些日晷使用晷針和節點測定日期和時間。
晷影器相對於晷面通常是固定的,但並非全都是這樣;在一些設計,如正投影日晷(analemmatic sundial),晷針是依月分(日期)移動的。如果晷針是固定的,在盤面上位於晷針垂直處下方的線稱為副晷針( substyle)[3],意思就是在晷針的下方。晷針與晷盤之間的角度稱為晷針高度,但此處的高度即為角度,是與一般不同的用法。在許多的牆面日晷,副晷針與正午線不相同(見下文)。在晷盤上的正午線和副晷針之間的角度距離稱為副晷針距離,距離在此處的意思也是角度,這又是一個不尋常的使用法。
傳統上,許多日晷都有銘文。這些銘文通常是警語或諷刺短詩的風格:有些是深沉的思考與反應時間和生命的短暫,但有時會展現日晷製造者的幽默或俏皮
[4][5]。
如果刻度盤上的時間線是等距離的直線,這個日晷會被稱為等角(equiangular)。多數的等角日晷都有固定的晷影器,並且晷針的指向會與地球的自轉軸對齊,同時接收影子的表面相對於軸也是對稱的;這些例子包括赤道式日晷、赤道弓形日晷、環形日晷、圓柱形日晷和圓錐形日晷。然而,其他的設計也有等角日晷,像是變心日晷中的朗伯日晷;正投影日晷的晷針也是可以移動的。
在南半球的日晷

在南半球澳大利亞伯斯的日晷,放大可以看見時間標誌是逆時針轉的。要注意的是讀出來的時間要參考均時差圖做修正。
在半球的某個特定緯度上的日晷,換到另一個半球在相對的緯度上要反轉過來使用。
在各自緯度上的日晷,換到另一個半球時要在相對的緯度上反過來才能使用在北半球正對著南方的垂直日晷放在南半球就成為要正對著北方的垂直日晷。水平日晷要確實的定位,就必須找到真正的北或南。這兩種日晷都要經過相同的程序來定位[6]。晷影器要設定正確的緯度,在南半球要指向真正的天球南極點,在北半球要指向真正的天球北極點[7]。時間線的數值也要反方向配置,在水平日晷是逆時針旋轉,而不是順時針方向[8]。
在一個半球設計的水平日晷的晷面,移到另一個半球時,可以在其餘角的緯度上做為正向垂直日晷的晷面。例如,在澳大利亞伯斯的緯度是南緯32度,則北緯58度(也就是90-32)正對著南方的垂直日晷,可以成為當地的水平日晷。蘇格蘭的伯斯位置稍微偏北一點,在當地正對著南方的垂直日晷的晷面,就會與澳大利亞伯斯的水平日晷的晷面一模一樣(忽略經度上的差異)。所以日晷在這兩地將會做著相同的工作。相應的,時間的標記在南半球的水平日晷是逆時針旋轉,而在北半球的垂直日晷也是如此(查看這篇文章頂部最初的兩張圖)。在北半球的水平日晷和南半球的垂直日晷,時間標記都是順時針旋轉的方向。
從日晷讀取時間的調整和鐘錶時間的計算
日晷的時間與鐘錶顯示的時間迥異,最常見的主要原因是日晷的指向不正確,或是時間線設置的不正確。例如,如前文所述的大批量產的商用水平日晷。日晷要能準確,這樣的日晷必須依照所在地的地理緯度來設計,它的晷針必須平行於地球的自轉軸;晷針必須對正真北和它的高度(其與水平面的角度)符合當地的地理緯度。若要調整晷針的高度,日晷通常可以略為"向上"或"向下"傾斜,同時還要維持晷針對正南北的指向[9]。
夏令時間(日光節約時間)的調整
世界上有一些地區有實行日光節約時間,通常是調整官方時間一小時。這種轉變必須添加到日晷的時間標示上,使它能夠與官方的時間一致。
時區(經度)修正
一個標準的時區通常蓋大約15°的經度範圍,在這個時區內的任何一點,無論是否在引用的經線上(通常都是15°的倍數),都是以那條經線的時間為準,但其實每相差一度時間就會有4分鐘的差異。在插圖上,在時區西側的日出和日落時間會比官方的時間晚,相較之下東側的則都會比較早。如果一個日晷的位置,就說它是位於參考經線的西方5°,因為太陽每小時繞著地球移動15°,它的時間讀數就會慢上20分鐘。這個差值在一整年中都是不變的常數。對等角日晷,像是赤道、球面、或朗伯日晷,可以通過旋轉晷面做出正確的修正,而無須更改晷影器的位置或方向。然而,這種方法不適用於其它形式的日晷,像是水平日晷,這種校正必須經由檢視才能適當的修正[來源請求]。
在最極端的情況下,時區的官方正午,包括日光節約時間,可以被提早3小時(太陽過中天的時間會是官方時間下午3點,3 pm)。出現這種情況的地區包括阿拉斯加的最西邊、中國和西班牙。
均時差的修正

均時差 -鐘錶上顯示的時間與日晷時間的差值。在軸上方的日晷時會比較快,在軸的下方日晷時則會比較慢。

The 赫斯特父子在1812年製作的日晷。使用一個圓形的尺規修正均時差。現在展示在德比博物館。
雖然,太陽繞地球的速率看起來是均勻一致的,但其實它不是完全一致。這是因為地球的軌道是橢圓的(事實上是地球繞著太陽的軌道不是完美的圓形),和地球的自轉軸相對於軌道面是傾斜的。因此,日晷的時間不同於標準時鐘時間。在一年當中,兩者之間的差值有4天為0,但在其它的日子不是太快,就是太慢,最大的差異可以達到15分鐘。這兒所說的差值就是均時差。這種修正是全球性的,與日晷所在地的緯度和形式無關。在很長的一段時間,幾個世紀或更久,它也會改變[10],這是因為地球的軌道和自轉速率都在慢慢的變化著。因此,幾個世紀前做的均時差圖和表,現在明顯的是不正確的。讀取一座古老日晷的時間,需要參照現在的均時差,而不是以當時製作在晷面上的來修正。
有一些日晷,會在日晷上提供校正均時差的飾板。更複雜的日晷,則自動將均時差的校正納入。例如,有些弓形赤道日晷備有一個小的輪子,可以設定一年的時間,依序旋轉赤道的弓,消除測量上的均時差。在其它的情況,時間線可以是曲線,或是赤道的弓像是一個花瓶,依據太陽在一年中的緯度變化,修正得到適當的時間[11]日光時間儀(heliochronometer)是一種精準的日晷,它在1763年由Philipp Hahn首度發展出來,並且大約在1827年由Abbé Guyoux加以改善[12]。它將視太陽時修正為平太陽時或其它的標準時間。日光時間儀通常可以顯示出一分鐘的時間。

逐日日晷(Sunquest sundial)。由Richard L. Schmoyer設計,坐落在美國德拉瓦州格林維爾的山古巴天文台39°48′36″N 75°37′48″W / 39.81000°N 75.63000°W / 39.81000; -75.63000
逐日日晷是Richard L. Schmoyer在1950年代設計的,受到日行跡啟發的晷影器將光影投射到眉月形的赤道晷面時間刻尺上。逐日日晷的精度和緯度都可以調整,自動修正了均時差,使其準確度和大多數的口袋手錶相似[13][14][15]。
許多類型的日晷都可以添加日行跡以修正視太陽時至平太陽時或其它的標準時間。通常它的時間線形狀會依據均時差成為類似"8"字形的圖形(日行跡)。這消彌了地球軌道輕微的偏心和轉軸傾斜所造成與平太陽時最大約15分鐘的時間差。這種形式的裝置會在複雜的水平和垂直日晷上看見。
準確的鐘被發明之前,在17世紀中葉,日晷是最普遍的計時器,並且被認為能準確的提供時間。均時差並未被使用。在好的時鐘發明之後,日晷仍然被認為是準確的,而時鐘是不準確的。均時差被用在與現在相反的方向上:修正時鐘顯示的時間,使它和日晷的一致。一些為時鐘精心製作的"鐘差",像是約瑟夫·威廉姆森在1720年註冊的機制,可以自動的完成這種修正(威廉姆森的裝置可能已經首次使用了差速齒輪裝置)。直到1800年以後,不正確的時鐘才被認為是正確的,而日晷時通常是錯誤的,而均時差才變成現在的形式。[來源請求]
日晷的標準設施
以適當角度傾斜安置的指針或稱為日規,是日晷上唯一需要經驗才能安裝的組件,因此大量生產用以顯示時間的庭園日晷,多半不能正確的顯示時間。在北緯45度或更高的緯度上也有許多日晷在使用。
日晷只要適當的調整晷針的傾斜角度,與地球的自轉軸平行,就能在不同的緯度上使用。也就是說晷針的末端在北半球必須指向天球的北極點,在南半球則要指向天球的南極點。而除了對準南北極點之外,在刻度盤上的時間標示角度不是等距的,也需要配合著調整。同樣的,刻度盤被扭曲的日晷也不能正確顯示的時間。

在塔甘羅格的地平日晷(1833年)
如果要顯示標準時間,日晷的設計就需要能轉動來調整經度造成的時間偏差,由於每15度是一個時區,所以轉動的最大範圍是向東或西7.5度,但是晷針仍然必須對準天球的北(南)極點。不過即使日晷就放置在時區的中心經度線上,還是要作均時差的校正。
要修正日光節約時間,刻度盤上就需要有兩組的數字或是使用修正表,而且還是要作時區內的經度偏差修正。而對有兩組數字的日晷,還有個非正式的規範,就是夏天的數字要用暖色表示,冬天的數字則用冷色來表示。
通常日晷顯示的真太陽時與鐘錶顯示的時間會有差異,這就是所謂的均時差,在一年之中最大的差值可以達到15分鐘。均時差的成因是地球的軌道是橢圓形的,還有自轉軸與軌道面之間的傾斜。所以一個好的日晷必須附上一張永久性對照表,最少要以月為單位來修正均時差。比較複雜的做法則是將時間的標示作成曲線,或是將晷針作成弧度,或是其他的方法將均時差直接修正。
晷影器軸固定的日晷

1959年在美國亞利桑那州落成的無憂無慮日晷,晷影器高達62-英尺(19-米),可能是當時在美國最大的日晷[16]。
一般用來觀測的日晷其晷影器和晷針都是固定在與地球的自轉軸對齊,指向真北或真南,並且與水平面的角度等於所在地的地理緯度。這根軸對齊天球軸,指向目前的天北極,也就是接近極星勾陳一,但並不是對準它。 以實例來說,天極的直下點或在真實北極,在赤道則是水平的指向真北。在印度齋浦,著名的日晷所在地晷影器和晷針的仰角是26°55",反映出當地的地理緯度。[來源請求]
在給定的任何一天,太陽相對於軸的轉動是均勻的,一小時大約15°,每24小時完成一個圓周(360°)。與軸對齊的線形晷影器所投下的陰影落在接收的盤面上,充滿了背向太陽的部分,同樣的也是每小時繞著天球的軸轉動15°。接收這個陰影的面通常是平坦的,但也可以是球、圓柱、圓錐,或其它的形狀。如果陰影落在與天球軸勻稱的面上(像是一個渾天儀或是赤道日晷),陰影在表面的移動就會是均勻的;日晷上的時間線就是等距的。然而,如果接收陰影的面不是對稱的(像是多數的水平日晷),陰影在面上的移動就不會是均勻的,時間線也就不會是等距的;一個例外是下面會介紹的朗伯日晷。
有些類型的日晷被設計成日規是固定的,但沒有對準天極,像是垂直的方尖碑。這種日晷將在#基於節點的日晷那一章節中介紹。
經驗值的時間線標記
以下各段中所顯示的公式可以為各種類型的日晷計算其時間線的位置。在某些情況下,計算很簡單;而有一些則是極其複雜的。還有一個辦法,可以在許多類型的日晷上找出時間線的位置,並且可以節省大量計算複雜的工作情況。[17] 這是以一個真實的日晷去經歷實際的測量,隔一定的時間標記出晷影器投影出的時間線。必須要考慮到均時差,以確保時間線的位置在一年中的位置都是獨立的。一個簡單的方法可以做到這一點,就是設置一個標準鐘,看著它顯示"日晷時間" [b],這個標準時間,[c],再加上那一天的均時差。[d][18]。日晷上的時間限標誌顯示的是晷針(不是晷影器整體)在每個整點時的陰影位置,並且以時間的數值標示。例如,當時間讀數是5:00,晷針的影子被標記為"5"(或羅馬數字的"V")。如果所有的時間標記不是在一天鐘完成的,則標準時鐘必須每一或二天就要調整均時差的變化。
赤道日晷

在北京故宮的赤道日晷。39°54′57″N 116°23′25″E / 39.9157°N 116.3904°E / 39.9157; 116.3904 (Forbidden City equatorial sundial) 晷針指向真北,與地平面的角度是當地的地理緯度。仔細查看full-size image顯示有類似蛛網狀的日期環和時間線。

最簡單的日晷就是赤道日晷(也稱為分點日晷),比較突出的特點是接收影子的晷面完全與晷影器和晷針垂直[19][20][21]。這個晷面稱為赤道面,因為它與地球和天球的赤道是平行的。如果晷影器是固定,並與地球的自轉軸對齊,視太陽繞著地球時,晷影器所投下的陰影會以均勻的速度在晷面上移動。由於太陽每24小時在天球上繞行360°,所以在赤道軌面上每小時的時間線就相當於15°的間距(360/24)。
- HE=15∘×t(hours){displaystyle H_{E}=15^{circ }times t(hours)}
均勻的時間間距使得這種類型的日晷很容易構建。如果晷面是不透明的材質,則兩面都需要標記上時間線,因為在冬季的影子會投影在晷面下方,而夏天的影子則投影在上方。使用半透明的晷面(例如玻璃),雖然兩面都需要時間線,但由於面對太陽這一面的時間線可以支援背面,所以時間線就只需要標誌在向陽的一面,但是時間的標誌(如果需要)由於面對太陽和背向太陽的不同,在兩面都需要標示。
這種盤面的另一個優點是均時差和夏令時可以通過每天適當的旋轉盤面,就可以簡單的修正。這是因為時間線是等距的圍繞著晷面排列。由於這個緣故赤道日晷常被選擇做為公開展示的日晷,它可以在合理的準確性內顯示真正的地方時間。
通過下面的公式可以修正均時差:
- Correction∘=EoT(minutes)+60×ΔDST(hours)4{displaystyle Correction^{circ }={frac {EoT(minutes)+60times Delta DST(hours)}{4}}}
在接近分點,也就是春分和秋分的日子,因為太陽幾乎就在赤道平面上,因此晷面上在一年當中的這些日子沒有清晰的影子可以觀察,這是設計上的一個缺點。
有時,赤道日晷上會加上一個節點,這讓日晷可以顯示出一年中的日期。在任何一天,節點的陰影會在晷面上以圓軌跡移動,由這個圓的半徑可以測量太陽的赤緯。節點通常設置在晷針的末端,但也可以設置在晷針的任何一處。古代有一種只有節點(沒有晷針)的變形赤道日晷,時間線有如蜘蛛網般的橫越過標誌日期的同心圓[22]。
水平日晷

在明尼蘇達州的水平日晷。2007年6月17日12:21。位置是北緯44°51'39.3",西經93°36'58.4"。
在水平日晷(也稱為庭園日晷)接收投影的面是對齊於地平面,而不像赤道日晷的晷針是垂直與平行於赤道的晷面[23][24][25]因此,陰影線在盤面上的轉動不是均勻的,時間線之間的間隔需要依據計算[26][27]
- tanHH=sinLtan(15∘×t){displaystyle tan H_{H}=sin Ltan(15^{circ }times t)}
或是:
- HH=tan−1[sinL×tan(15∘×t)]{displaystyle H_{H}=tan ^{-1}[sin Ltimes tan(15^{circ }times t)]}
此處的L 是日晷的地理緯度(也是晷針相對於地平面的角度),HH{displaystyle H_{H}}



在英國倫敦邱宮外的水平日晷明細圖。
水平日晷的主要優點是容易讀取,和太陽全年都能照射在它的晷面上。所有的時間線都交會在晷影器上的晷針與地坪盤面相交的點。因為晷針對正著真北,與地平盤面的夾角等於日晷所在地的地理緯度L。在一個緯度上的日晷,若設計成晷面可以調整俯仰角,就可以適用在不同的其它緯度。例如,一個為緯度40°設計的水平日晷,如果晷面可以向上傾斜5°,只要晷針依然對齊著真北,就可以在緯度45° 上使用。[來源請求]
許多觀賞用的日晷都是以北緯45度設計的。一些大量產的庭園日晷沒有正確的計算與刻畫時間線,因此永遠不能正確的顯示時間(除了顯示正午時刻)。名義上,一個地方的時區標準寬度是15度,但可能會因為地理或政治的邊界而有所調整。一個日晷的晷面可以繞著晷針(晷針必須對準天極)旋轉,以在本地的時區內調整經度差。在大多數的情況下,只要在7.5度的範圍內向東或向西旋轉2至3度就足夠了,但這將導致日晷沒有相同角度時間線的差異。要正確的顯示夏令時,一個盤面就需要兩套數值或是修正表。一個不成文的慣例是夏天的數值使用暖色調,冬天的數值使用冷色調[來源請求]
由於時間線的分布不是等距的,因此均時差的修正不能以晷針為軸來旋轉盤面。這種類型日晷的均時差通常要在晷面的空位上或附近製作修正表。
水平日晷最常見的場所是庭園、教堂和墓園等公共區域。
垂直日晷

在英國諾福克霍頓廳的兩個垂直日晷52°49′39″N 0°39′27″E / 52.827469°N 0.657616°E / 52.827469; 0.657616 (Houghton Hall vertical sundials)。左邊和右邊的日晷正面分別對著南方和東方。兩個晷針是相互平行的,它們對地平面的角度等於地理緯度。面向東方的日晷是個時間線相互平行的極日晷,晷面與晷針是平行的。
一般的垂直日晷,接收陰影的平面是與垂直面一致的;一如往常,晷影器上的晷針是與地球的自轉軸對齊[19][28][29]。如同水平日晷,晷影的線在盤面上的移動是不均勻的;這種日晷不是等角。如果垂直的晷面是朝向正南方,時間線的角度就要由不同的公式去描述[30][31]
- tanHV=cosLtan(15∘×t){displaystyle tan H_{V}=cos Ltan(15^{circ }times t)}
此處的L是日晷的地理緯度,HV{displaystyle H_{V}}

晷面垂直於地面,並且正對著東、西、南或北方的被稱為垂直正向日晷[32][33]。它被廣泛的以為,即使在受人尊敬的出版品中也是如此:無論白天的日照時間有多長,在一天當中,一個垂直日晷的晷面被陽光照到的時間不會超過12小時[34]。然而,凡事都有例外,在熱帶面向極區的垂直日晷(也就是說在北回歸線和赤道之間面向北方的垂直日晷),在夏至前後的短暫時間,在日出到日落之間,晷面接受陽光照射的時間會超過12小時。例如,在北緯20度,當6月21日夏至這一天,陽光照射在朝向北方的垂直日晷盤面上的時間是13小時又21分鐘[35]。不是正向南方的垂直日晷(在北半球),取決於它們面對的方向和一年中的日期,每一天受到陽光照射的時間可能會很明顯的少於12小時。例如,面向東方的垂直日晷只會在正午之前受到陽光的照射,在正午之後,陽光就造不到它的晷面。面相正東方或正西方的垂直日晷都是極日晷,會在後面說明。面向北方的垂直日晷是不很罕見的,因為只能在春季和夏季顯示時間,而且除非是在熱帶,將無法在正午前後顯示時間(即使在熱帶,也只能在仲夏,也就是夏至前後顯示)。對於非正向垂直日晷的晷面 -面對非基本方向- 設置晷針和時間線的數學變得更加複雜;通過觀察可能更容易標示時間線,但是至少晷針的設置還是需要先經由數學計算;這種日晷稱為斜向日晷[36][37][38]。

在捷克布拉格梅圖耶河畔新城的"雙"日晷;觀測者幾乎面向正北。
垂直日晷通常安置在建築物的牆面上,例如市政廳、圓頂和教會的高塔,它們在那裡很容易就能從遠方看到。在某些情況,在矩形建築的四面都會設置垂直日晷,以提供整個白天的時間。在牆上的晷面可能會彩繪,或以石塊鑲嵌;晷影器往往是單一的金屬棒或以三腳架固定的金屬棒。如果建築的牆面只是朝向南方,但不是正對著南方,晷影器就不能沿著正午線設置,而且時間線也需要修正。由於晷影器上的晷針必須平行於地球的自轉軸,並且永遠要指向真北,也就是它與地平面的夾角必須是當地的地理緯度;在正南向垂直日晷,晷針與晷面的夾角就是地理緯度的餘角,也就是90°減去地理緯度[39]。
口袋日晷
這種可以摺疊的德國日晷有一整排的晷影器,可以將晷針正確的調整至任何的緯度。當陰影越過日晷,較小的晷面會顯示義大利和巴比倫的時間。晷面還可以顯示一天的長度和太陽在黃道12宮的位置[來源請求]。
極日晷

在澳洲墨爾本墨爾本天象廳的極日晷。
極日晷,接收晷影器上晷針投影的平面與晷針是平行的[40][41][42]。因此,當太陽相對於晷針垂直移動時,影子永遠落在晷影器另一側的晷面上。如同晷影器一樣,時間線也是與地球自轉軸對齊的。當陽光將近平行於晷面時,晷影的移動會非常迅速,時間線的間距也會很大。朝向東面或西面的正向垂直日晷就是極日晷。然而,極日晷的晷面必不需要垂直;它所需要的只是與晷影器上的晷針平行。因此,晷面的傾斜角度(相對於地平面)就是地理緯度,而晷影器也有相同傾斜角度的就是極日晷。在晷面上的時間線X的垂直距離可以由下面的公式描述:
- X=Htan(15∘×t){displaystyle X=Htan(15^{circ }times t)}
此處的H 是晷針在晷面上的高度,t是相對於極日晷中心的時間(單位為時)。中心時間是晷針的影子直接落在晷面上的時間;對東向日晷,中心時間是早上6點,西向日晷的中心時間是下午6點;前述的傾斜極日晷,中心時間是正午。當 t接近距離中心時間 ±6小時,X的間距會趨近於+∞;這時陽光將變成平行於晷面。
垂直斜向日晷
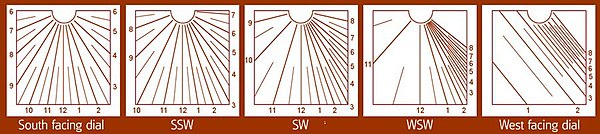
傾斜對日晷時間線造成的影響。在北緯51°,設計成朝向正南方的日晷(最左邊)顯示從早上6點至晚上6點所有的時間線,並且都對稱於12點的正午時間線和收斂於規根。相較之下,朝向西方的日晷(最右邊)時間線是平行的,並且只有下午的時間。在中間的分別朝向西南南方、西南方和西南西方,時間線不與12點的正午線對稱,而且上午時間線的間隔比下午的寬闊。

在土耳其伊斯坦堡法齊赫清真寺一大一小的兩個日晷,可以追溯到16世紀後期。它位於西南方的外牆上,方位角是52° N。
斜向日晷是任何非水平設置,盤面沒有正對著東、西、南、或北的日晷[36][43][38]。像其他的日晷一樣,晷影器上的晷針還是需要與地球的自轉軸對齊,但是時間線不再會與正午線對稱。對垂直日晷,正午線和其它時間線的角度HVD{displaystyle H_{text{VD}}}

- tanHVD=cosLcosDcot(15∘×t)−sosinLsinD{displaystyle tan H_{text{VD}}={frac {cos L}{cos Dcot(15^{circ }times t)-s_{o}sin Lsin D}}}
此處的L{displaystyle L}



- tanHV=cosLtan(15∘×t){displaystyle tan H_{text{V}}=cos Ltan(15^{circ }times t)}
當沒有對正四方為之一時,晷影器的副晷針就不會與正午線對齊。副晷針和正午時間線的角度B{displaystyle B}
- tanB=sinDcotL{displaystyle tan B=sin Dcot L}
如果垂直日晷正對南方或北方(D=0∘{displaystyle D=0^{circ }}


晷影器的高度,也就是晷針與晷面的夾角G{displaystyle G}
- sinG=cosDcosL{displaystyle sin G=cos Dcos L}
[45]
斜倚日晷

在南半球的垂直日晷,晷面朝北,與雙曲線的赤緯線和時間線。通常在這個緯度(位於回歸線內)的垂直日晷在夏至前後的正午時段無法使用。
前述的日晷都有對正著地球自轉軸的晷影器,並將影子投映在平面上。如果這個平面既不垂直也不平行於赤道,這種日晷就稱為斜倚日晷或傾斜日晷[46]。例如,設置在朝南方屋頂上的就可能是這種日晷。要設置這種日晷的時間線時,只要將上面計算水平日晷的公式稍加修改[47]:
- tanHRV=cos(L+R)tan(15∘×t){displaystyle tan H_{RV}=cos(L+R)tan(15^{circ }times t)}
此處的R{displaystyle R}

有些作者使用更特別的名稱來描述接收影子的平面方向。如果平面的正面朝下向著地面,它被稱為傾斜或是前傾;許多作者也經常引用為斜倚、傾斜或前傾,當作一般的斜向日晷。在後者的情況下,朝向太陽的那一面相對於地平面也常見它是傾斜的。
在這種情況下,因為I = 90° + R,經常可以看見時角的公式被寫成:
- tanHRV=sin(L+I)tan(15∘×t){displaystyle tan H_{RV}=sin(L+I)tan(15^{circ }times t)}
晷針和日晷盤面,B,在這種類型的日晷是:
- B=90∘−(L+R){displaystyle B=90^{circ }-(L+R)}
Or :
- B=180∘−(L+I){displaystyle B=180^{circ }-(L+I)}
Declining-reclining dials/ Declining-inclining dials
經驗法
由於上述計算的複雜性,設計這種類型的日晷要達到實際的使用目的是困難的,而且容易出錯。因此建議在現場實測時間線是較務實的做法。在真實的日晷,以鐘錶顯示的時間找到晷針投影對應的時間線,更容易正確地做得完善[17]。請參閱前文的經驗值的時間線標記。
球面日晷

在比利時法蘭德斯哈瑟爾特自治市的赤道弓形日晷 50°55′47″N 5°20′31″E / 50.92972°N 5.34194°E / 50.92972; 5.34194 (Hasselt equatorial bow sundial)。光線穿過窄槽(隙縫)形成隨著太陽均勻轉動的光束落在弓形的圓環上。時間線是等距離分布;在這張圖片中,地方太陽時大約是15:00(下午3點)。 在9月10日,在窄槽中焊接的一個小球造成的陰影落在中心的時間帶上。
接收影子的面不一定需要平面,而可以是任何的形狀,但前提是製造商能順利的標示時間線。如果晷針與地球的自轉軸對齊,球面的形狀就很方便,因為時間線是等距離畫分,就如同前面的赤道日晷,這種日晷是等角的。這是環形和赤道弓形日晷背後的規則[48][49][50]。 然而,有些等角的日晷,如下面描述的朗伯日晷,是依據其它的規則。
在赤道弓形日晷,晷影器是棒狀、槽線、或拉出與天球軸平行的線。面對的是一個相當於赤道球,並且在其內側表面飾有斑紋的半圓。使用不會因為溫度而變化的因鋼,製作數米寬的成對因鋼瓦的這種類型日晷,在第一次世界大戰之前的法國用於維持列車的時間[51]。
最精確兩個赤道弓形日晷是用大理石製作的,建置在印度齋浦爾的簡塔·曼塔天文台[52][53]。集合在這兒的日晷和其它天文儀器是瑪哈茹阿佳萨瓦伊·杰伊·辛格二世在1727年至1733年間,建成他的新首都齋浦爾之後建造的。較大的那個赤道弓形日晷被稱為Samrat Yantra(最優秀的儀器),高有27公尺,它的影子每秒鐘移動1毫米,或大約是每分鐘一隻手的寬度(6公分)。
圓柱形、圓錐形、和其它非平面的日晷

在比利時比特根巴赫的精密日晷(精確度 = ±30 秒)。 50°25′23″N 6°12′06″E / 50.4231°N 6.2017°E / 50.4231; 6.2017 (Belgium) (Google Earth)
其他非平面表面也可以用於接收晷影器的影子。
做為優雅的另類,晷針(可以是一個小孔或是在圓周上的一條狹縫)可以設置在圓柱體或球體上,而不是在其中央的對稱軸。
在這種情況下,時間線同樣是等間距的,但由於幾何上的圓周角定理,角度通常是2倍。這是一些現代日晷的基礎,但在遠古時代也有用過[e]。
在另一種變異的極軸對齊的圓柱型日晷,圓柱的日晷可以呈現出像螺旋絲帶一樣的盤面,薄薄的晷影器可以在它的中心,也可以在它的邊緣。
變心日晷(Movable-gnomon sundials)
日晷也可以設計成晷影器在一年中的每一天都放置在不同的位置。換言之,晷影器的位置相對於中心時間線的位置各不相同。晷影器和晷針不需要與天球極點對齊,甚至可能完全垂直於地面(正投影日晷)。這些日晷與晷影器固定的日晷結合,在沒有其它的資源下可以確定真北;而且只有在兩個日晷都顯示相同的時間時,並且只有在這樣的情況下這兩個日晷才是正確的對齊[來源請求]。
通用赤道環形日晷

通用環形日晷。這種日晷在圖的左上角有條吊線,可以在垂直的子午環上更改懸掛點以配合當地的地理緯度。中心的棒可以旋轉,以讓陽光可以穿過中心的小孔,落在圖中水平的赤道環上。參見在公開註解的標籤.
通用赤道環形日晷(universal equinoctial ring dial,通常簡稱為環形日晷或環晷,然而這樣會使意義含糊不清)是一種便於攜帶的環狀日晷[55],或許是受到航海星盤啟發的一種日晷[56]。它可能是威廉·奧特雷德大約在1600年發明的,在歐洲極為常見[57]。
在最簡單的形式,晷針只是允許陽光落在赤道環時間線上的細縫。一如往常,晷針需要對齊地球的自轉軸;因此,使用者必須讓日晷垂直的子午線環上適當的點指向真北。這種日晷的盤面可以加上一個更複雜的中央短棒,來取代簡單的狹縫晷針。這種短棒有時會附加上一組德式環,在短棒的兩個端點上有樞軸可以扭轉;短棒上有個穿孔的滑塊,可以依據月分和日期調整位置。通過旋轉短棒,讓陽光穿過滑塊上的小孔落在赤道環上來確定時間。 這迫使使用者必須旋轉致個儀器,校正垂直的圓環與子午圈一致。
不使用時,赤道環和子午環可以摺疊在一起,收成一個小盤。
在1610年,愛德華·賴特在通用環形日晷上加裝磁羅盤,創造了海環。這讓水手可以在單一的步驟中確定時間和磁偏角[58]。
正投影日晷

在比利時佛蘭德斯 哈瑟爾特自治市的荷肯路德修道院花園裡,設置在子午線上的正投影日晷。
正投影日晷是具有垂直晷影器,而時間線位於橢圓形上的一種水平日晷。晷面上沒有時間線將橢圓上的時間標記和任何一天的日期連結以讀取時間。晷影器或晷針沒有固定,而必須每天改變位置才能準確的只是當天的時間。正投影日晷有時會設計成以人本身作為晷影器。
在低緯度,以人做為晷影器的正投影日晷在夏季並不實用。以北緯27度為例,一個身高6.6-英尺(2.0-米)的人在夏至日的正午的影子度長只有1⁄3-英尺(0.10-米)[59]。
在中緯度,這個橢圓形和時間標記的大小可以達到6公尺,這樣觀察者頭(晷針)的影子都能落在時間標記的附近。
朗伯日晷
朗伯日晷(Lambert dials)是另一種晷影器(晷針)必須移動的變心日晷[60]。相對於橢圓形的正投影日晷,朗伯日晷的時間線類似於赤道日晷、球形或圓柱日晷,是均勻等角度的圓形刻畫。朗伯日晷的晷針不是垂直的,而是朝向極點傾斜一個角度,而這個角的大小是α=45-(ψ/2),此處的ψ是所在地的地理緯度。因此,在北緯40°的朗伯日晷的晷針的傾角是朝向北方傾斜25°。要讀取正確的時間,晷針也必須配合太陽的赤緯在子午線上移動適當的距離Y:
- Y=Rtanαtanδ{displaystyle Y=Rtan alpha tan delta ,}
此處的R是朗伯日晷的半徑,δ是一年當中太陽在當時的赤緯。
以高度為準的日晷
高度日晷是測量太陽在天空中的高度,而不是測量太陽相對於地球自轉軸的時角。它們不必指向真北,而是朝向著太陽,並且通常都是垂直豎立著。太陽的高度角由節點、晷影器的尖端、或是光點的位置來顯示。
高度日晷,是以節點落在一年中隨著日期更換的一組時間曲線上的位置來讀取時間。許多這種高度日晷是建構在高度密集的計算,也有案例是有許多的方位晷面。但是斗篷日晷(capuchin dials,如下所述)是做圖和使用圖形的方式。
高度日晷的缺點(不便):
由於太陽的高度在與正午的間隔相等時(例如上午9:00與下午3:00),有著相同的高度,使用者必須知道是在上午還是下午。以下午3:00來說,這不會發生問題,但是與正午相隔15分鐘的11:45和12:15,使用者就可能會無法區分出來。
此外,高度日晷在正午都不太正確,因為在接近正午時,太陽的高度變化會較為緩慢。
許多這種日晷只是便於攜帶和使用。相較於其它的日晷,許多高度日晷的設計只適用於單一的緯度。但是斗篷日晷(如下所述)有可以調整緯度的版本[61]。
梅奧爾&梅奧爾的日晷之書敘述通用的斗篷日晷。
人影日晷
一個人的影子(或任何垂直的物體)長度可以用來測量太陽的高度、方位和時間[62]。古老的神學家比德給了一張以人影高度估計時間的表,使用的單位是英尺,其中一個假設是和尚的身高是它腳的長度的6倍。影子的長度與地理緯度和每年的時間都有關聯。例如,影子的長度在夏季的中午最短,而在冬季的月份會最長。
傑弗里·喬叟在坎特伯里故事集(短篇故事合集)的'牧師的故事'中,多次的引用此方法。
[f]
使用一根長度固定的等效類型的日晷被稱為backstaff dial。
牧羊人日晷 - 時間棍

19世紀藏族牧羊人的時間棍。
牧羊人日晷,也稱為牧羊人圓柱日晷[63][64]、 柱日晷(pillar dial)、圓筒日晷(cylinder dial) 或 chilindre — 是一種可攜帶的圓柱型日晷,有一根小刀形狀的晷影器呈直角伸出[65]。它通常被用繩子或弦吊住,所以圓柱體是垂直的。晷影器可以被扭轉一個月或一天以顯示在圓柱的表面,以修正日晷的均時差。整個日晷可以用的的串繩來扭轉,以讓晷影器朝向太陽,而圓柱保持垂直。在圓柱上的陰影尖端指示時間。圓柱上的時間曲線讓人可以讀取時間。牧羊人日晷有些是中空的,所以在不使用時可以將晷影器摺疊在內。
在莎士比亞的亨利六世,第三部曾引用牧羊人日晷: [g];在其它的文學作品也有[h]。
圓柱形的牧羊人日晷可以展開成平面。在一種簡單的版本[66],正面和背面各有三列,對應於太陽赤緯大致相同的月份(6-7月、5月和8月、4月和9月、3月和10月、2月和11月、以及1月和12月)。每一列的頂端有一個可以插入晷影器的孔,一根竹釘。通常在每一列上下只會標示兩個時間:一個是正午,另一個是午前或午後約2小時。
時間棍、鐘叉(clock spear),[63]或牧羊人的時棍[63]都是基於和日晷相同的原則製作晷面[63][64]。時間棍會為一年中不同的階段中,刻上8個垂直的時間尺度,每個不同的尺度對應一年中不同月份的白晝長度。任何的讀取不僅是一天中的時刻,也取決於緯度和一年中的季節[64]。做為晷影器的竹釘插入頂端適合季節的孔洞或晷面,並且要轉向朝著太陽,影子能落在時間的標尺上,讓影子的末端指示時間[63]。
環日晷(Ring dials)
環日晷,也稱為阿基坦(Aquitaine)或穿孔環日晷(perforated ring dial),環是垂直懸掛並以側面朝向太陽[67]。一束陽光會穿過圓環上的小孔,而落在刻在環內側的時間曲線上。若要調整均時差,通常小孔會在較鬆動的內環,以便可以調整小孔以反映當前的月份。
卡片日晷(斗篷日晷)
卡片日晷是另一種形式的高度日晷[68]。卡片以一側的邊緣朝向太陽傾斜並且對齊,讓一縷陽光穿過孔徑到達一個指定的點,從而確定太陽的高度。一條有足夠重量的繩串穿過卡片上的小孔攜帶著串珠或結點垂向下方。串珠在時間線上的位置顯示了時間。在更複雜的版本,像是斗篷日晷,還有時間線,但是只有一組,也就是不會隨季節調整。相反的,足夠重量繩串的掛孔位置可以隨著季節調整。
斗篷日晷是建置和使用圖形的方式,而不是像水平或赤道日晷直接測量時角,或是像一些高度和方位日晷計算時間線。
除了普通的斗篷日晷之外,還有一種可以調整緯度的通用斗篷日晷。
以節點為基礎的日晷
摺疊式日晷

可攜帶的摺疊式日晷
一種便於攜帶的日晷稱為摺疊式日晷,他有以絞鏈結合在一起的兩個小晷面,通常會折疊起來放在平整的小盒子內,以方便放在口袋中。晷針則是在兩晷面之間的帶子,當帶子被扯緊拉直時,兩個晷面會互相垂直,一個面形成垂直式日晷,另一個面則是水平式的日晷。 最考究的晷面材料是以白色的象牙製作,塗飾上來自中國的暗色真漆,晷針則是黑色的絲綢、亞麻或大麻纖維。
如果在晷針上正確的位置打個結作為節點,摺疊式日晷也能當作日曆來使用,至少可以顯示農作的適當時機。
讓兩個晷面以不同的角度結合(會產生不同的投影),摺疊式日晷便可以自行調整。當兩晷面顯示出相同的時間,而且絞鏈是水平的,摺疊式日晷指示的是當地的視太陽時。另外,當絞鏈朝向北方(在北半球時),摺疊式日晷被旋轉了一個角度,晷針才能與地球的自轉軸平行,則當正午、日出與日落時,摺疊式日晷的時間不會受到緯度改變的影響,但是在早上9點和下午3點,緯度每偏差1度,在兩個晷面上的時間便會相差4分鐘(肇因於日晷在錯誤的緯度上)。
這表示摺疊式日晷可以像指南針一樣來使用,甚至可以測量緯度。也些摺疊式日晷附有小的鉛錘和分度器來讀取正確的緯度;也有些附有指南針,可以測量地理上的特徵。在古代,大型的(1公尺以上的)摺疊式日晷曾經被用於航海上。

於1742年在都柏林以黃銅製造的攜帶式日晷。
18世紀早期的攜帶式日晷
這一種形式的日晷以黃銅製造,直徑約8公分,當攜帶外出時有黃銅的蓋子保護(圖中未顯示)。有些特點使他能保持足夠的精確度,如附有指南針可以正確的定出北方,時間的刻度為5分鐘。這個日晷是1742年由在都柏林的一位數學儀器製造商Gabriel Stokes製造的。
等高儀日晷(Elevation sundial)
等高儀可以顯示正確的日期,是使用在導航與天文學上的日晷。
在設計上是一個平坦的小圓環,有一個小把手,或是像錶鏈上的飾物,還是小裝飾。. 當以把手將環懸吊起來時,小孔會在環的內側投下陰影,經由環內的標示可以顯示時間,但使用者自己必須知道現在是上午還是下午。通常這個小孔被設置在一片可以滑動和鎖住,用來調整日期的金屬片上。
在現代,美國的特種部隊仍然喜歡在他們的刀片上刻上一個簡易的日晷,以便在手錶失效時仍能知道時間。

在魯特琴上的日晷,大約在 1612年。

建築在 巴黎的旅者日晷,可能是Butterfield在18世紀末葉製作的
精密日晷 (日光天文鐘)
一種精密的日晷,被稱為日光天文鐘,可以校正視太陽時為平太陽時或是其他的標準時。
日光天文鐘的精確度可以達到與世界時的差異少於一分鐘,相關的討論請參考Sundial Accuracy。
赤道弓形日晷
傳統上的日光天文鐘是赤道弓形日晷,作為晷針的是一根伸展開來與地球自轉軸平行的棒狀物,晷面是在在內側標示上了時間的標線半圓形的環,環的直徑在2~3公尺,材質是不會受溫度影響而膨脹或收縮的因鋼,這是在第一次世界大戰前在法國發明的鋼材,使鐵路整年都能暢通無阻。
讀取時間的方法是最簡單的,只要看相兩個希臘瓶的弓形晷針在赤道環上的投影。[1] 瓶型的陰影落在時間線上的位置可以指出一年中正確的日期和太陽高度的改變。
目前最巨大的赤道弓形日晷是位在印度齋浦以石材製造的日晷,是一系列天文設施中的一件。
古希臘的日晷
在古希臘使用一種稱為pelekinon的日晷(軸像,明顯的因為等時線和日期線的形狀,暗示這種古老的日晷是雙軸的pelekus)。 晷針是標尺或是極,豎立在平面上或是半球型的晷面上,標尺頂端的投影在平面的晷面上掃掠出雙曲線的軌跡,或在球面上畫出圓弧。這種日晷的優點是可以確實的標記出一年中所有季節的
時日。
地球儀式日晷
地球儀式日晷可以將時間修正為平太陽時或其他的標準時間,他們通常會按照地球儀的均時差將等時線繪成8字形。 均時差的成因是地球的軌道是橢圓形的,還有自轉軸與軌道面之間的傾斜,在一年之中最大的差值可以達到15分鐘。
在公共的廣場非常適合安置這種精確的日晷,在旗竿上的球可以作為晷針上的節點,晷面則可以鑲嵌在道路上。
反射日晷
牛頓 利用南向的窗戶發明了反射日晷,他在窗台上放置一小片的鏡子,然後將天花板和牆面當成晷面,繪製上時間的標記。鏡子好比是晷針上的節點,反射陽光成為一個亮點。這提供了一個巨大、精確且完全可以校正的日晷,使用的材料最少,而且不佔用到任何的空間。 這種設計可以簡單的作成年曆表。
地平式日晷
最後,介紹一種有趣的經過改變但還能正確顯示時間,晷面作成心型的地平式日晷(心臟的形狀),基本上還是一種庭園日晷。心臟線是橫過晷面。陰影橫過心臟線的邊緣處是讀取時間標記的位置,在這兒可以讀到盤面上所顯示的時間。雖然晷面不能移動,但只要轉動晷面下的等角時間標示,這個日晷可以調整為夏令時間。
數位日晷
數位化的日晷利用光和影來"寫"時間,以數字或文字來取代在不同地點的時間標記。一種設計是在屏幕上使用兩個平行的遮罩,由陽光進入的樣式來判斷時間和日期。
註解
^ 在專業論文中,"gnomon"這個字也被用來描述節點至晷盤的垂直距離(高度),稱為"晷影器高"(晷影器高度,不是日晷整體的高度);晷影器與晷盤的交點稱為"晷影器根"(gnomon root)。
^ 顯示日晷時間的時鐘一定要與日晷在相同的地點。
^ 嚴格的說,應該是地方平時而不是使用標準時間。然而,使用標準時間會更加有用,因為就無需再修正時區和經度。
^ 當"日晷時"超前"鐘錶時"均時差是正值,反過來是負值。參見前面的均時差的修正圖。例如,均時差是-5分鐘,標準時間是9:40,則日晷的時間是9:35
^ 在麻塞諸塞州的衛斯理學院發現的一個半圓柱體日晷就是個例子[54]。
^
Chaucer:as in his Parson's Tale. It was four o'clock according to my guess,
Since eleven feet, a little more or less,
my shadow at the time did fall,
Considering that I myself am six feet tall.
^ Henry VI, Part 3:O God! methinks it were a happy life
To be no better than a homely swain;
To sit upon a hill, as I do now,
To carve out dials, quaintly, point by point,
Thereby to see the minutes, how they run--
How many makes the hour full complete,
How many hours brings about the day,
How many days will finish up the year,
How many years a mortal man may live.
^ For example, in the Chaucer's Canterbury Tales, the monk says, "Goth now your wey," quod he, "al stille and softe,
And lat us dyne as sone as that ye may;
for by my chilindre it is pryme of day."
參考文獻
^ Moss, Tony. How do sundials work. British Sundial society. [21 September 2013]. (原始内容存档于August 2, 2013).This ugly plastic ‘non-dial’ does nothing at all except display the ‘designer’s ignorance and persuade the general public that ‘real’ sundials don’t work.
^ Trentin, Guglielmo; Repetto, Manuela. Using Network and Mobile Technology to Bridge Formal and Informal Learning. Elsevier. 2013-02-08. ISBN 9781780633626 (英语).
^ 3.03.13.2 British Sundial, Society. BSS Glossary. [2011-05-02]. (原始内容存档于2007-10-10).
^ Rohr 1965, pp. 126–129.
^ Waugh 1973, pp. 124–125.
^ Michelle B. Larson. Making a sundial for the Southern hemisphere. [2008-07-11].
^ Michelle B. Larson. Making a sundial for the Southern hemisphere. [2008-07-11].
^ British Sundial, Society. The Sundial Register. [2014-10-13].
^ Waugh 1973, pp. 48–50.
^ Karney, Kevin. Variation in the Equation of Time (PDF).
^ The Claremont, CA, Bowstring Equatorial. Photo Info. [2008-01-19]. (原始内容存档于2008-04-22).
^ Christopher St. J.H. Daniel. Sundials. Osprey Publishing. 4 March 2008: 47– [25 March 2013]. ISBN 978-0-7478-0558-8.
^ Waugh, Albert. Sundials: Their Theory and Construction. New York: Dover Publications. 1973: 34.
^ Cousins, Frank W. Sundials: The Art and Science of Gnomonics. New York: Pica Press. 1973: 189–195.
^ Stong, C.L. The Amateur Scientist. Scientific American. 1959, 200 (5): 185–198.
^ The Sundial and Geometry p 38. 互联网档案馆的存檔,存档日期2016-03-04.
^ 17.017.1 Waugh 1973, pp. 106–107.
^ Waugh 1973, p. 205.
^ 19.019.1 Rohr 1965, pp. 46–49.
^ Mayall & Mayall 1938, pp. 55–56, 96–98, 138–141.
^ Waugh 1973, pp. 29–34.
^ Schaldach K. The arachne of the Amphiareion and the origin of gnomonics in Greece. Journal of the History of Astronomy. 2004, 35: 435–445. ISSN 0021-8286. doi:10.1177/002182860403500404.
^ Rohr 1965, pp. 49–53.
^ Mayall & Mayall 1938, pp. 56–99, 101–143, 138–141.
^ Waugh 1973, pp. 35–51.
^ Rohr 1965, p. 52.
^ Waugh 1973, p. 45.
^ Mayall & Mayall 1938, pp. 557–58, 102–107, 141–143.
^ Waugh 1973, pp. 52–99.
^ Rohr 1965, p. 65.
^ Waugh 1973, p. 52.
^ Rohr 1965, pp. 54–55.
^ Waugh 1973, pp. 52–69.
^ Waugh 1973, p. 83.
^ Morrissey, David. Worldwide Sunrise and Sunset map. [28 October 2013].
^ 36.036.1 Rohr 1965, pp. 55–69.
^ Mayall & Mayall 1938, p. 58.
^ 38.038.1 Waugh 1973, pp. 74–99.
^ Waugh 1973, p. 55.
^ Rohr 1965, p. 72.
^ Mayall & Mayall 1938, pp. 58, 107–112.
^ Waugh 1973, pp. 70–73.
^ Mayall & Mayall 1938, pp. 58–112, 101–117, 1458–146.
^ 44.044.1 Rohr 1965, p. 79.
^ Mayall & Mayall 1938, p. 138.
^ Rohr (1965), pp. 70–81; Waugh (1973), pp. 100–107; Mayall and Mayall (1994), pp. 59–60, 117–122, 144–145.
^ Rohr (1965), p. 77; Waugh (1973), pp. 101–103; Capt. Samuel Sturmy. The Art of Dialling. London: Unknown publisher. 1683.
^ Rohr 1965, pp. 114, 1214–125.
^ Mayall & Mayall 1938, pp. 60, 126–129, 151–115.
^ Waugh 1973, pp. 174–180.
^ Rohr 1965, p. 17.
^ Rohr 1965, pp. 118–119.
^ Mayall & Mayall 1938, pp. 215–216.
^ Mayall Mayall, p. 94.
^ Waugh 1973, p. 157.
^ Swanick, Lois Ann. An Analysis Of Navigational Instruments In The Age Of Exploration: 15th Century To Mid-17th Century, MA Thesis, Texas A&M University, December 2005
^ Turner 1980, p. 25.
^ May, William Edward, A History of Marine Navigation, G. T. Foulis & Co. Ltd., Henley-on-Thames, Oxfordshire, 1973, ISBN 0-85429-143-1
^ Analemmatic sundials: How to build one and why they work by C.J. Budd and C.J. Sangwin
^ Mayall & Mayall 1938, pp. 190–192.
^ Mayall & Mayall 1965, p. 169.
^ Rohr (1965), p. 15; Waugh (1973), pp. 1–3.
^ 63.063.163.263.363.4 National Maritime Museum; Lippincott, Kristen; Eco, Umberto; Gombrich, E. H. The Story of Time. London: Merrell Holberton in association with National Maritime Museum. 1999: 42–43. ISBN 1-85894-072-9.
^ 64.064.164.2 St. Edmundsbury, Borough Council. Telling the story of time measurement: The Beginnings. [2008-06-20]. (原始内容存档于August 27, 2006).
^ Rohr (1965), pp. 109–111; Waugh (1973), pp. 150–154; Mayall and Mayall, pp. 162–166.
^ Waugh (1973), pp. 166–167.
^ Rohr (1965), p. 111; Waugh (1973), pp. 158–160; Mayall and Mayall (1994), pp. 159–162.
^ Rohr (1965), p. 110; Waugh (1973), pp. 161–165; Mayall and Mayall (1994), p. 166–185.
- 《日晷设计原理》,吴振华著,上海交通大学出版社,2001年6月。
Sundials: Their Theory and Construction, Albert E. Waugh, Dover Publications, Inc., 1973, ISBN 978-0-486-22947-8.- "Sundials Old and New", A.P.Herbert, Methuen & Co. Ltd, 1967.
外部連結
维基共享资源中相关的多媒体资源:日晷 |
Sunbeams and Sundials – Guide to the sun, the seasons and sundials.
A virtual sundial.- Sundials
Digital sundial patent, with description of related designs. The patent was filed June 1995 [2].
MarsDial – Sundials carried on Mars rovers Spirit (MER-A) and Opportunity (MER-B).
Sundial links – Collection of sundial links.
Sundials – Tutorial about sundials, incl plan for folded paper sundial which can be xeroxed.- Keppel Henge
Nijmegen sundial generator – Generate the dial of a horizontal/vertical/cylindrical sundial online.
《关于如何弥补大理石日晷建立缺陷的书籍》是报时和日晷1319左右的阿拉伯语手稿。
建造倾斜日晷所用数表的计算方法专著是另一个阿拉伯语手稿,从16世纪的数学计算用于创建日晷。它是由SIBT的AL-Maridini的。
参见
- 圭表
- 月晷
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
|



![{displaystyle H_{H}=tan ^{-1}[sin Ltimes tan(15^{circ }times t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb53d9480d130ffd58d4d2fe57bc7f66e8b6ff04)










