PID控制器
PID控制器(比例-积分-微分控制器),由比例单元(P)、积分单元(I)和微分单元(D)组成[1]。透过Kp,Ki和Kd三个参数的设定。PID控制器主要适用于基本上线性,且动态特性不随时间变化的系统。

PID控制器的方塊圖
PID控制器是一个在工业控制应用中常见的反馈回路部件。这个控制器把收集到的数据和一个参考值进行比较,然后把这个差别用于计算新的输入值,这个新的输入值的目的是可以让系统的数据达到或者保持在参考值。PID控制器可以根据历史数据和差别的出现率来调整输入值,使系统更加准确而稳定。
PID控制器的比例单元(P)、积分单元(I)和微分单元(D)分別對應目前誤差、過去累計誤差及未來誤差。若是不知道受控系統的特性,一般認為PID控制器是最適用的控制器[2]。藉由調整PID控制器的三個參數,可以調整控制系統,設法滿足設計需求。控制器的響應可以用控制器對誤差的反應快慢、控制器過衝的程度及系統震盪的程度來表示。不過使用PID控制器不一定保證可達到系統的最佳控制,也不保證系統穩定性。
有些應用只需要PID控制器的部份單元,可以將不需要單元的參數設為零即可。因此PID控制器可以變成PI控制器、PD控制器、P控制器或I控制器。其中又以PI控制器比較常用,因為D控制器對回授雜訊十分敏感,而若沒有I控制器的話,系統不會回到參考值,會存在一個誤差量。
目录
1 反馈回路基础
2 歷史及應用
3 理论
3.1 比例控制項
3.1.1 穩態誤差
3.2 積分控制項
3.3 微分控制項
4 參數調試
4.1 穩定性
4.2 最佳性能
4.3 各方法的簡介
4.4 人工調整
4.5 齊格勒-尼科爾斯方法
4.6 PID調試軟體
5 PID控制的限制
5.1 線性
5.2 雜訊對微分器的影響
6 PID演算法的修改
6.1 積分飽和
6.2 PI控制器
6.3 不動作區
6.4 設定值的步階變化
6.5 前饋控制
6.6 無衝擊運轉
7 串級PID控制器
8 其他PID的形式及其表示法
8.1 理想的PID及標準形PID
8.2 倒數增益
8.3 只針對過程變數進行微分控制
8.4 只針對過程變數進行微分及比例控制
8.5 PID控制器的拉氏轉換
8.6 PID的極零點對消
8.7 串級型或交互型
8.8 離散化的控制器
9 虛擬码
10 参见
11 注释
12 参考文献
13 外部链接
反馈回路基础
PID回路是要自动实现一个操作人员用量具和控制旋钮進行的工作,这个操作人员会用量具测系统输出的结果,然后用控制旋钮来调整这个系统的输入,直到系统的输出在量具上显示稳定的需求的结果,在旧的控制文档里,这个过程叫做“复位”行为,量具被称为“测量”,需要的结果被称为“設定值”而設定值和测量之间的差别被称为“误差”。
一个控制回路包括三个部分:
- 系统的传感器得到的测量结果
- 控制器作出决定
- 通过一个输出设备来作出反应
控制器从传感器得到测量结果,然后用需求结果减去测量结果来得到误差。然后用误差来计算出一个对系统的纠正值来作为输入结果,这样系统就可以从它的输出结果中消除误差。
在一个PID回路中,这个纠正值有三种算法,消除目前的误差,平均过去的误差,和透過误差的改变来预测将来的误差。
比如说,假如利用水箱在为植物提供水,水箱的水需要保持在一定的高度。可以用传感器来检查水箱里水的高度,这样就得到了测量结果。控制器会有一个固定的用户输入值来表示水箱需要的水面高度,假设这个值是保持65%的水量。控制器的输出设备会连在由马达控制的水阀门上。打开阀门就会给水箱注水,关上阀门就会让水箱里的水量下降。这个阀门的控制信号就是控制变量。
PID控制器可以用来控制任何可被测量及可被控制变量。比如,它可以用来控制温度、压强、流量、化学成分、速度等等。汽车上的巡航定速功能就是一个例子。
一些控制系统把数个PID控制器串联起来,或是连成网络。这样的话,一个主控制器可能会为其他控制输出结果。一个常见的例子是马达的控制。控制系統會需要马达有一个受控的速度,最後停在一个确定的位置。可由一個子控制器用来管理速度,但是这个子控制器的速度是由控制马达位置的主控制器来管理的。
连合和串联控制在化学过程控制系统中相當常见。
歷史及應用

PID控制理論是由觀察舵手的動作而來
PID控制器可以追溯到1890年代的调速器設計[2][3]。PID控制器是在船舶自动操作系統中漸漸發展。1911年Elmer Sperry開發的控制器是最早期PID型控制器的其中之一[4],而第一個發表PID控制器理論分析論文的是俄裔美国工程師尼古拉斯·米诺尔斯基(Minorsky 1922)。米诺尔斯基當時在設計美國海軍的自动操作系統,他的設計是基於對舵手的觀察,控制船舶不只是依目前的誤差,也考慮過去的誤差以及誤差的變化趨勢[5],後來米诺尔斯基也用數學的方式加以推導[6]。他的目的是在於穩定性,而不是泛用的控制,因此大幅的簡化了問題。比例控制可以在小的擾動下有穩定性,但無法消除穩態誤差,因此加入了積分項,後來也加入了微分項。
當時在新墨西哥號戰艦上進行測試,利用控制器控制舵的角速度,利用PI控制器可以角度誤差維持在±2°以內,若加上D控制,角度誤差維持在±1/6°,比最好的舵手還要好[7]。
不過因為海軍人員的抗拒,海軍那時候未使用這套系統,在1930年代也有其他人作出類似的研究。
在自動控制發展的早期,用機械設備來實現PID控制,是由槓桿、彈簧、阻尼及質量組成,多半會用壓縮氣體驅動。氣動控制器還一度是工業上的標準。
電子的類比控制器可以用電晶體、真空管、電容器及電阻器組成。許多複雜的電子系統中常會包括PID控制,例如磁碟的讀寫頭定位、電源供應器的電源條件、甚至是現代地震儀的運動偵測線路。現代電子控制器已大幅的被這些利用單晶片或FPGA來實現的數位控制器所取代。
現代工業使用的PID控制器多半會用PLC或有安装面板的數位控制器來實現。軟體實現的好處是相對低廉,配合PID實現方式調整的靈敏度很大。在工業鍋爐、塑膠射出機械、烫金机及包裝行業中都會用到PID控制。
變化的電壓輸出可以用PWM來實現,也就是固定週期,依要輸出的量去調整週期中輸出高電位的時間。對於數位系統,其時間比例有可能是離散的,例如週期是二秒,高電位時間設定單位為0.1秒,表示可以分為20格,精度5%,因此存在一量化誤差,但只要時間解析度夠高,就會有不錯的效果。
理论
PID是以它的三种纠正算法而命名。受控變數是三种算法(比例、積分、微分)相加後的結果,即為其輸出,其輸入為误差值(設定值減去测量值後的結果)或是由误差值衍生的信號。若定義u(t){displaystyle u(t)}
- u(t)=MV(t)=Kpe(t)+Ki∫0te(τ)dτ+Kdddte(t){displaystyle mathrm {u} (t)=mathrm {MV} (t)=K_{p}{e(t)}+K_{i}int _{0}^{t}{e(tau )},{dtau }+K_{d}{frac {d}{dt}}e(t)}
其中
Kp{displaystyle K_{p}}:比例增益,是調適參數
Ki{displaystyle K_{i}}:積分增益,也是調適參數
Kd{displaystyle K_{d}}:微分增益,也是調適參數
e{displaystyle e}:誤差=設定值(SP)- 回授值(PV)
t{displaystyle t}:目前時間
τ{displaystyle tau }:積分變數,數值從0到目前時間t{displaystyle t}
用更专业的话来讲,PID控制器可以視為是频域系统的滤波器。在计算控制器最终是否会达到稳定结果时,此性質很有用。如果数值挑选不当,控制系统的输入值会反复振盪,这导致系统可能永远无法达到预设值。
PID控制器的一般转移函数是:
H(s)=Kds2+Kps+Kis+C{displaystyle H(s)={frac {K_{d}s^{2}+K_{p}s+K_{i}}{s+C}}},
其中C是一个取决于系统带宽的常数。
比例控制項

不同比例增益Kp下,受控變數對時間的變化(Ki和Kd維持定值)
比例控制考慮当前誤差,误差值和一个正值的常数Kp(表示比例)相乘。Kp只是在控制器的输出和系统的误差成比例的时候成立。比如说,一个电热器的控制器的比例尺范围是10°C,它的目標值是20°C。那么它在10°C的时候会输出100%,在15°C的时候会输出50%,在19°C的时候输出10%,注意在误差是0的时候,控制器的输出也是0。
比例控制的輸出如下:
- Pout=Kpe(t){displaystyle P_{mathrm {out} }=K_{p},{e(t)}}
若比例增益大,在相同誤差量下,會有較大的輸出,但若比例增益太大,會使系統不穩定。相反的,若比例增益小,若在相同誤差量下,其輸出較小,因此控制器會較不敏感的。若比例增益太小,當有干擾出現時,其控制信號可能不夠大,無法修正干擾的影響。
穩態誤差
比例控制在誤差為0時,其輸出也會為0。若要讓受控輸出為非零的數值,就需要有一個穩態誤差或偏移量[a]。穩態誤差和比例增益的成反比。若加入一偏置,或是加入積分控制,可以消除穩態誤差。
積分控制項
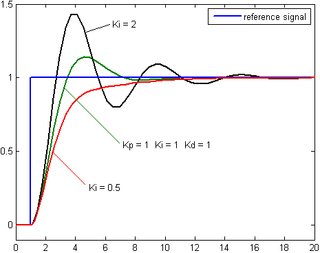
不同積分增益Ki下,受控變數對時間的變化(Kp和Kd維持定值)
积分控制考慮过去誤差,將误差值过去一段时间和(误差和)乘以一个正值的常数Ki。Ki从过去的平均误差值来找到系统的输出结果和预定值的平均误差。一个简单的比例系统会震盪,会在预定值的附近来回变化,因为系统无法消除多余的纠正。通过加上负的平均误差值,平均系统误差值就会漸漸减少。所以,最终这个PID回路系统会在設定值稳定下来。
積分控制的輸出如下:
- Iout=Ki∫0te(τ)dτ{displaystyle I_{mathrm {out} }=K_{i}int _{0}^{t}{e(tau )},{dtau }}
積分控制會加速系統趨近設定值的過程,並且消除純比例控制器會出現的穩態誤差。積分增益越大,趨近設定值的速度越快,不過因為積分控制會累計過去所有的誤差,可能會使回授值出現過衝的情形。
微分控制項
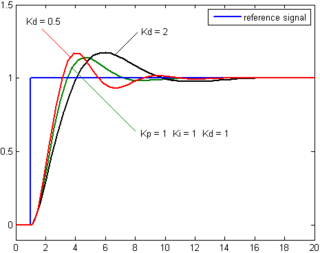
不同微分增益Kd下,受控變數對時間的變化(Kp和Ki維持定值)
微分控制考慮将来誤差,计算误差的一阶导,并和一个正值的常数Kd相乘。这个导数的控制会对系统的改变作出反应。导数的结果越大,那么控制系统就对输出结果作出更快速的反应。这个Kd参数也是PID被称为可预测的控制器的原因。Kd参数对减少控制器短期的改变很有帮助。一些实际中的速度缓慢的系统可以不需要Kd参数。
微分控制的輸出如下:
- Dout=Kdddte(t){displaystyle D_{mathrm {out} }=K_{d}{frac {d}{dt}}e(t)}
微分控制可以提昇整定時間及系統穩定性[8][9]。不過因為純微分器不是因果系统,因此在PID系統實現時,一般會為微分控制加上一個低通濾波器以限制高頻增益及雜訊[10]。實际上較少用到微分控制,估計PID控制器中只有約20%有用到微分控制[10]。
參數調試
PID的參數調試是指透過調整控制參數(比例增益、積分增益/時間、微分增益/時間)讓系統達到最佳的控制效果。穩定性(不會有發散性的震盪)是首要條件,此外,不同系統有不同的行為,不同的應用其需求也不同,而且這些需求還可能會互相衝突。
PID只有三個參數,在原理上容易說明,但PID參數調試是一個困難的工作,因為要符合一些特別的準則,而且PID控制有其限制存在。歷史上有許多不同的PID參數調試方式,包括齊格勒-尼科爾斯方法等,其中也有一些已申請專利。
PID控制器的設計及調試在概念上很直覺,但若有多個(且互相衝突)的目標(例如高穩定性及快速的暫態時間)都要達到的話,在實際上很難完成。PID控制器的參數若仔細的調試,會有很好的效果,相反的,若調適不當,效果會很差。一般初始設計常需要不斷的電腦模擬,並且修改參數,一直達到理想的性能或是可接受的妥協為止。
有些系統有非線性的特性,若在無載下調試的參數可能無法在滿載下動作,可以利用增益規劃的方式進行修正(在不同的條件下選用不同的數值)。
穩定性
若PID控制器的參數未挑選妥當,其控制器輸出可能是不穩定的,也就是其輸出發散,過程中可能有震盪,也可能沒有震盪,且其輸出只受飽和或是機械損壞等原因所限制。不穩定一般是因為過大增益造成,特別是針對延遲時間很長的系統。
一般而言,PID控制器會要求響應的穩定,不論程序條件及設定值如何組合,都不能出現大幅振盪的情形,不過有時可以接受臨界穩定的情形[來源請求]。
最佳性能
PID控制器的最佳性能可能和針對過程變化或是設定值變化有關,也會隨應用而不同。
兩個基本的需求是調整能力(regulation,干擾拒絕,使系統維持在設定值)及命令追隨 (設定值變化下,控制器輸出追隨設定值的反應速度)。有關命令追隨的一些準則包括有上昇時間及整定時間。有些應用可能因為安全考量,不允許輸出超過設定值,也有些應用要求在到達設定值過程中的能量可以最小化。
各方法的簡介
有許多種調試PID控制器參數的方法,最有效的方式多半是建立某種程序,再依不同參數下的動態特性來調試參數。相對而言人工調試其效率較差,若是系統的響應時間到數分鐘以上,更可以看出人工調試效率的不佳[來源請求]。
調試方法的選擇和是否可以暫時將控制迴路「離線」有關,也和系統的響應時間有關。離線是指一個和實際使用有些不同的條件(例如不加負載),而且控制器的輸出只需考慮理論情況,不需考慮實際應用。在線調試是在實際應用的條件,控制器的輸出需考慮實際的系統
。若控制迴路可以離線,最好的調試方法是對系統給一個步階輸入,量測其輸出對時間的關係,再用其響應來決定參數[來源請求]。
| 方法 | 優點 | 缺點 |
|---|---|---|
| 人工調試 | 不需要數學,可以在線調試 | 需要有經驗的工程師[來源請求] |
| 齊格勒-尼科爾斯方法 | 被證實有效的方法,可以在線調試 | 會影響製程,需要試誤,得到的參數可能使響應太快[來源請求] |
| 軟體工具 | 調適的一致性,可以在線調試或離線調試,可以配合计算机自动设计,包括閥及感測器的分析,可以在下載前進行模擬,可以支援非穩態(NSS)的調試 | 需要成本或是訓練[11] |
| Cohen–Coon | 好的程序模型 | 需要一些數學,需離線調試,只對一階系統有良好效果[來源請求] |
人工調整
若需在系統仍有負載的情形進行調試(線上調試),有一種作法是先將Ki{displaystyle K_{i}}









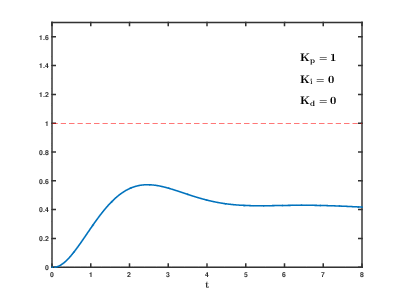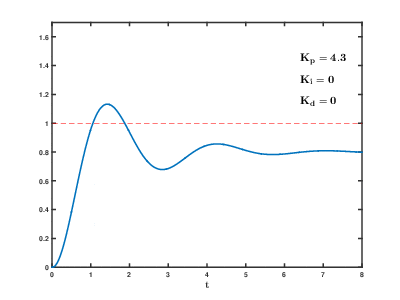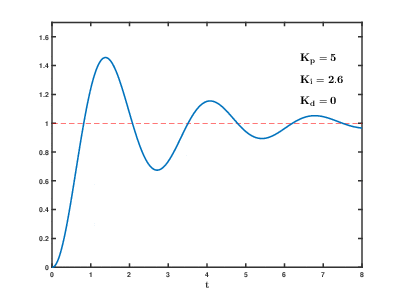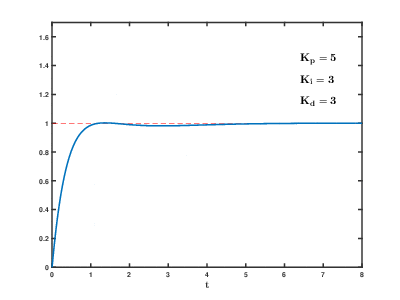
調整PID參數對其步階響應的影響
調整PID參數對系統的影響如下
| 調整方式 | (on) 上升时间 | 超调量 | 安定时间 | 稳态误差 | 稳定性[10] |
|---|---|---|---|---|---|
| ↑ Kp | 減少 ↓ | 增加 ↑ | 小幅增加 ↗ | 減少 ↓ | 變差 ↓ |
| ↑ Ki | 小幅減少 ↘ | 增加↑ | 增加 ↑ | 大幅減少↓↓ | 變差↓ |
| ↑ Kd | 小幅減少 ↘ | 減少↓ | 減少↓ | 變動不大→ | 變好 ↑ |
齊格勒-尼科爾斯方法
齊格勒-尼科爾斯方法是另一種啟發式的調試方式,由John G. Ziegler和Nathaniel B. Nichols在1940年代導入,一開始也是將Ki{displaystyle K_{i}}



| 控制器種類 | Kp{displaystyle K_{p}}  | Ki{displaystyle K_{i}}  | Kd{displaystyle K_{d}}  |
|---|---|---|---|
P | 0.50Ku{displaystyle 0.50{K_{u}}}  | - | - |
PI | 0.45Ku{displaystyle 0.45{K_{u}}}  | 1.2Kp/Pu{displaystyle 1.2{K_{p}}/P_{u}}  | - |
PID | 0.60Ku{displaystyle 0.60{K_{u}}}  | 2Kp/Pu{displaystyle 2{K_{p}}/P_{u}}  | KpPu/8{displaystyle {K_{p}}{P_{u}}/8}  |
PID調試軟體
大部份現代的工業設備不再用上述人工計算的方式調試,而是用PID調試及最佳化軟體來達到一致的效果。軟體會收集資料,建立模型,並提供最佳的調試結果,有些軟體甚至可以用參考命令的變化來進行調試。
數學的PID調試會將脈衝加入系統,再用受控系統的頻率響應來設計PID的參數。若是響應時間要數分鐘的系統,建議用數學PID調試,因為用試誤法可能要花上幾天才能找到可讓系統穩定的參數。最佳解不太容易找到,有些數位的迴路控制器有自我調試的程序,利用微小的參考命令來計算最佳的調試值。
也有其他調試的公式,是依不同的性能準則所產生。許多有專利的公式已嵌入在PID調試軟體及硬體模組中[12]。
一些先進的PID調試軟體也可以有演算法可以在動態的情形下調整PID迴路,這類軟體會先將程序建模,給微擾量,再根據響應計算參數。
PID控制的限制
PID控制可以應用在許多控制問題,多半在大略調整參數後就有不錯的效果,不過有些應用下可能反而會有差的效果,而且一般無法提供最佳控制。PID控制的主要問題是在於其為回授控制,係數為定值,不知道受控系統的資訊,因此其整理性能常常是妥協下的結果。在沒有受控系統模型的條件下,PID控制最佳的控制器[2],但若配合系統模型,可以有進一步的提昇。
當PID控制器單獨使用時,若因應用需求,需調整PID迴路增益使控制系統不會過衝,其效果有可能很差。PID控制器的缺點還包括無法處理受控系統的非線性、需在反應時間及调整率之間妥協、無法針對參數的變動而反應(例如系統在暖機後特性會改變)、以及大擾動下的波形落後。
PID控制器最顯著的提昇是配合前饋控制,加入有關系統的資訊,只用PID控制器來控制誤差。另外,PID控制器也有一些小幅的改善方式,例如調整參數(增益規劃或是依性能進行適應性的調整)、提昇性能(提高取樣率、精度及準度,若有需要加入低波濾波器),或是用多個串接的PID控制器。
線性
PID控制器常見的問題是在於其線性且對稱的特性,若應用在一些非線性的系統,其效果可能會有變化。以暖通空調中常見的溫度控制,可能是採用主動加熱(用加熱器加熱),但冷卻是使用被動冷卻(不加熱,自然冷卻),其冷卻速度比加熱速度慢很多,輸出若有過衝,下降速度很慢,因此PID控制需調整為不會過衝的過阻尼,以減少或避免過衝,但這也延長了整定時間,使性能變差。
雜訊對微分器的影響
微分器的問題在於對量測或程序產生的高頻雜訊會有放大效果,因此會對輸出造成大幅的變動。因此真實的控制器不會有理想的微分器,只有一個有限頻寬的微分器或高通濾波器。一般為了移除高頻的雜訊,會在量測時加入低通濾波器,若低通濾波器和微分器對消,濾波效果也就受限了,因此低雜訊的量測設備相當重要。實務上可以使用中值滤波器,調昇濾波效率及實際上的性能[13]。有時可以將微分器關閉,對控制性能的影響不大,此時稱為PI控制器。
PID演算法的修改
基本的PID演算法在一些控制應用的條件下有些不足,需進行小幅的修改。
積分飽和
積分飽和是理想PID演算法實現時常見的問題。若設定值有大的變動,其積分量會有大幅的變化,大到輸出值被上下限限制而飽和,因此系統會有過衝,而且即使誤差量符號改變,積分量變小,但輸出值仍被上下限限制,維持在上限(或下限),因此輸出看似沒有變化,系統仍會持續的過衝,一直要到輸出值落在上下限的範圍內,系統的回授量才會開始下降。此問題可以用以下方式處理:
- 在程序變數離開可控制範圍時,暫停積分。
- 讓積分值限制在一個較小的上下範圍內。
- 重新計算積分項,使控制器輸出維持上下限之間的範圍內[14]。
PI控制器

PI控制器的方塊圖
PI控制器(比例-積分控制器)是不用微分單元的PID控制器。
控制器的輸出為
- KPΔ+KI∫Δdt{displaystyle K_{P}Delta +K_{I}int Delta ,dt}
其中Δ{displaystyle Delta }
Δ=SP−PV{displaystyle Delta =SP-PV}.
PI控制器可以用Simulink或Xcos之類的軟體進行建模,方式是使用「flow chart」圖框,其中用以下的拉氏運算子:
- C=G(1+τs)τs{displaystyle C={frac {G(1+tau s)}{tau s}}}
其中
G=KP{displaystyle G=K_{P}}= 比例增益
G/τ=KI{displaystyle G/tau =K_{I}}= 積分增益
G{displaystyle G}
微分單元對輸入中的高頻信號格外敏感,PI控制器因為沒有微分單元,在訊號雜訊大時,在穩態時會更加穩定。但對狀態快速變化的反應較慢,因此相較於調適到最佳值的PID控制器,PI控制器會較慢到達設定值,受干擾後也比較慢恢復到正常值。
PDF控制(pseudo-derivative feedback control)可以視為是PI控制器的變體,比例控制器的輸入由誤差值改為回授值[15]。
不動作區
許多PID迴路是控制機械元件(例如閥)。機械保養是一筆可觀的費用,磨損會使得機械在有輸入信號時出現靜摩擦或是不動作區,都會導致控制性能的下降。機械損耗的速度主要和設備多常改變其狀態有關。若磨損是主要考量的話,PID迴路可以有輸出的遲滯現象以減少輸出狀態的改變。若變化小,仍在不動作區內,讓控制器的輸出維持上一次的值。變化要大到超過不動作區,實際的狀態才會隨之變化。
設定值的步階變化
若系統的設定值有步階變化,比例單元和微分單元也會有對應的變化,特別是微分單元對於步階變化的輸出特別的大,因此有些PID演算法會配合以下的修改來處理設定值的變化。
- 設定值斜坡變化
- 此修改方式下,設定值會用線性或是一階濾波的方式,由原始值變到新的值,避免因為步階變化產生的不連續。
- 只對程序變數(回授量)微分
- 此修改下,PID控制器只針對量測的程序變數(PV)微分,不對誤差微分。程序變數是實際的物理量,較不易有瞬間的變化,而誤差可能因為設定值的步階變化而有瞬間變化。這也是一種簡單的設定值加權法。
- 設定值加權
- 設定值加權分別調整在比例單元及微分單元中的誤差量,誤差量的設定值乘以一個0到1之間的加權,積分單元的誤差量需使用真實的設定值,以避免穩態誤差。這兩個參數不影響對負載變化及量測雜訊的響應,可以提昇對設定點變化的響應。
前饋控制
PID控制器若再配合前饋控制(開迴路控制),可以再提昇其控制性能。在前饋控制中考慮系統的已知資訊(例如理想加速度或是慣量),再將輸出加到PID控制器的控制輸出,以提昇整體的系統性能。前饋量可能是控制輸出主要的部份,而PID控制器只用來補償目標值和開迴路控制器輸出之間的誤差。因為前饋輸出不會受到回授的影響,因此也不會造成系統的振盪,可以在不影響穩定性的條件下提昇系統的響應。前饋可以依目標值及其他量測到的干擾量來產生,目標值加權是一種簡單的前饋控制方式。
例如,在大部份的運動控制系統中,為了要使機械負載加速,致動器要產生更大的力。若用速度環的PID控制器來控制負載速度,比較理想的方式是先得到理想的瞬間加速度值,適量調整加權後再加到PID的輸出中。因此控制器輸出中有一部份是不隨機械速度而改變的輸出,再用PID根據實際輸出和目標的差異去增加或是減少輸出。這類有前饋控制的PID控制器可以加快控制系統的反應速度。
無衝擊運轉
有時PID控制器會規劃為無衝擊(bumpless)的特性,在參數變化時重新計算適當的積分累計值,使輸出不會因參數變化有不連續的改變[16]。
串級PID控制器
二個PID控制器可以組合在一起,得到較佳的效果,這稱為串級PID控制。以兩個PID控制器組成的串級PID控制為例,其中一個PID控制器在外迴路,控制像液面高度或是速度等主要的物理量,另一個PID控制器是內迴路,以外迴路PID控制器的輸出做為其目標值,一般是控制較快速變化的參數,例如流量或加速度等。若利用串級PID控制,可以增加控制器的工作頻率,並降低其時間常數。
例如一個溫控的循環水浴設備有二個串級的PID控制器,分別有各自的熱電偶溫度感測器。外迴路的控制器控制水溫,其感測器距加熱器很遠,直接量測整體水溫,其誤差量是理想水溫及整體水溫的差值。外迴路PID控制器的输出即為內迴路控制器的目標值,內迴路控制器控制加熱器,其感測器是在加熱器上,其誤差量是加熱器的理想溫度及量測到溫度的差值,其輸出會使加熱器維持在設定值附近。
內外迴路控制器的參數可能會差很多,外迴路的PID控制器有較長的時間常數,對應所有的水加熱或是冷卻需要的時間。內迴路的PID控制器反應會比較快。每個控制器可以調整到符合其真正控制的系統,例如水槽中所有的水,或是加熱器本身。
其他PID的形式及其表示法
理想的PID及標準形PID
工業上常看到PID控制器,而許多工業相關資料中看到的都是「標準形」的PID,其中比例增益Kp{displaystyle K_{p}}


- MV(t)=Kp(e(t)+1Ti∫0te(τ)dτ+Tdddte(t)){displaystyle mathrm {MV(t)} =K_{p}left(,{e(t)}+{frac {1}{T_{i}}}int _{0}^{t}{e(tau )},{dtau }+T_{d}{frac {d}{dt}}e(t)right)}
其中
Ti{displaystyle T_{i}}為積分時間
Td{displaystyle T_{d}}為微分時間
在標準形中,每一個參數有其明確的物理意義,輸出是根據現在誤差、過去誤差及未來誤差而決定,加上微分項可以預測若控制系統不改變的話,Td{displaystyle T_{d}}


在理想的平行式PID中,其方程如下:
- MV(t)=Kpe(t)+Ki∫0te(τ)dτ+Kdddte(t){displaystyle mathrm {MV(t)} =K_{p}{e(t)}+K_{i}int _{0}^{t}{e(tau )},{dtau }+K_{d}{frac {d}{dt}}e(t)}
其中的增益和標準形PID係數的關係是:Ki=KpTi{displaystyle K_{i}={frac {K_{p}}{T_{i}}}}

倒數增益
許多情形下,PID控制器處理的變數是無因次的量,是某個最大值的比例,介於0到100%之間,而轉換為實際物理量(如泵浦速率或是水加熱的功率)是在PID控制器外,而這些控制變數是有因次的物理量(例如溫度)。此時Kp{displaystyle K_{p}}

只針對過程變數進行微分控制
在大部份的商業控制系統中,是用過程變數取代誤差作為微分項的輸入,其原因是當目標值有不連續變化時,微分控制會產生很大的突波,若目標值不變,改變過程變數的效果和改變誤差相同,因此有些PID控制器會用過程變數作為微分項的輸入,不會影響控制器控制過程變數,抗雜訊的能力。
- MV(t)=Kp(e(t)+1Ti∫0te(τ)dτ−TdddtPV(t)){displaystyle mathrm {MV(t)} =K_{p}left(,{e(t)}+{frac {1}{T_{i}}}int _{0}^{t}{e(tau )},{dtau }-T_{d}{frac {d}{dt}}PV(t)right)}
只針對過程變數進行微分及比例控制
大部份的商業控制系統也提供選擇,讓過程變數作為微分控制及比例控制的輸入,因此誤差只作為積分控制的輸入,這也不會影響控制器控制過程變數,抗雜訊的能力。
上述的修改可以避免目標值有不連續變化時,輸出值有對應不連續的變化,若目標值有步階變化,這項調整就相當重要。
- MV(t)=Kp(−PV(t)+1Ti∫0te(τ)dτ−TdddtPV(t)){displaystyle mathrm {MV(t)} =K_{p}left(,{-PV(t)}+{frac {1}{T_{i}}}int _{0}^{t}{e(tau )},{dtau }-T_{d}{frac {d}{dt}}PV(t)right)}
也有些雙自由度(2-DoF)PID控制架構除了一般的PID控制外,再加上只針對過程變數進行的微分及比例控制,再分別用增益進行調整,目標是同時對目標步階響應以及雜訊抑制都有良好的性能[17]。
PID控制器的拉氏轉換
有關會將PID控制器進行拉氏轉換:
- G(s)=Kp+Kis+Kds=Kds2+Kps+Kis{displaystyle G(s)=K_{p}+{frac {K_{i}}{s}}+K_{d}{s}={frac {K_{d}{s^{2}}+K_{p}{s}+K_{i}}{s}}}
PID控制器的拉氏轉換也代表著控制器的傳遞函數,因此可以確認整體系統的傳遞函數。
PID的極零點對消
PID控制器可以寫成以下的形式
- G(s)=Kds2+KpKds+KiKds{displaystyle G(s)=K_{d}{frac {s^{2}+{frac {K_{p}}{K_{d}}}s+{frac {K_{i}}{K_{d}}}}{s}}}
若受控設備的傳遞函數如下:
- H(s)=1s2+2ζω0s+ω02{displaystyle H(s)={frac {1}{s^{2}+2zeta omega _{0}s+omega _{0}^{2}}}}
又令
- KiKd=ω02{displaystyle {frac {K_{i}}{K_{d}}}=omega _{0}^{2}}
- KpKd=2ζω0{displaystyle {frac {K_{p}}{K_{d}}}=2zeta omega _{0}}
則
- G(s)H(s)=Kds{displaystyle G(s)H(s)={frac {K_{d}}{s}}}
因此若受控設備有不穩定的極點,看似可以用此方式消除,不過實際上有些差異,由干擾到輸出的閉迴路傳遞函數中仍有不穩定的極點,因此仍可能會發散。
串級型或交互型
另一種PID控制器的表示法為串級型(series)或稱為交互型(interacting)
- G(s)=Kc(τis+1)τis(τds+1){displaystyle G(s)=K_{c}{frac {(tau _{i}{s}+1)}{tau _{i}{s}}}(tau _{d}{s}+1)}
其中參數和標準型的參數有以下的關係
Kp=Kc⋅α{displaystyle K_{p}=K_{c}cdot alpha }, Ti=τi⋅α{displaystyle T_{i}=tau _{i}cdot alpha }
- Td=τdα{displaystyle T_{d}={frac {tau _{d}}{alpha }}}
而
α=1+τdτi{displaystyle alpha =1+{frac {tau _{d}}{tau _{i}}}}.
上述作法可表示為二個串級的PD控制器及PI控制器,在早期類比電路的時代較容易實現,雖然控制器已經數位化,不過仍有些維持此形式。
離散化的控制器
若要在微處理機(MCU)或是FPGA中實現PID控制或是分析其性能,就需要將控制器離散化[18]。一階微分可以用後向有限差分表示,積分項也離散化,若取樣時間為Δt{displaystyle Delta t}
- ∫0tke(τ)dτ=∑i=1ke(ti)Δt{displaystyle int _{0}^{t_{k}}{e(tau )},{dtau }=sum _{i=1}^{k}e(t_{i})Delta t}
微分項可近似為
- de(tk)dt=e(tk)−e(tk−1)Δt{displaystyle {dfrac {de(t_{k})}{dt}}={dfrac {e(t_{k})-e(t_{k-1})}{Delta t}}}
因此PID控制器的離散化可以將u(t){displaystyle u(t)}

- u(tk)=u(tk−1)+Kp[(1+ΔtTi+TdΔt)e(tk)+(−1−2TdΔt)e(tk−1)+TdΔte(tk−2)]{displaystyle u(t_{k})=u(t_{k-1})+K_{p}left[left(1+{dfrac {Delta t}{T_{i}}}+{dfrac {T_{d}}{Delta t}}right)e(t_{k})+left(-1-{dfrac {2T_{d}}{Delta t}}right)e(t_{k-1})+{dfrac {T_{d}}{Delta t}}e(t_{k-2})right]}
其中Ti=Kp/Ki,Td=Kd/Kp{displaystyle T_{i}=K_{p}/K_{i},T_{d}=K_{d}/K_{p}}
虛擬码
以下是一段實現PID演算法的虛擬码:[19]
previous_error = 0
integral = 0
start:
error = setpoint - measured_value
integral = integral + error*dt
derivative = (error - previous_error)/dt
output = Kp*error + Ki*integral + Kd*derivative
previous_error = error
wait(dt)
goto start
此例中有兩個變數在迴圈前需初始化為0,然後開始迴圈。目前的誤差(error)是用目前目標值(setpoint)減去系统反馈值(measured_value)而得,然後再進行積分和微分運算,比例項、積分項及微分項乘以各自參數後得到輸出(output)。在實際系統中,這會透過數位類比轉換器轉換為類比訊號,作為受控系統的控制量。目前的誤差量及積分會儲存,以便下次計算微分及積分時使用,程式會等待dt秒後開始,迴圈繼續進行,透過類比數位轉換器讀取新的系统反馈值及目標值,再計算誤差量及輸出[19]。
参见
- 控制理论
- 反馈
- 不穩定
- 振荡
注释
^ 唯一的例外是目標值恰好是比例增益等於0時的受控輸出。
参考文献
^ Li, Y., Ang, K.H., and Chong, G.C.Y. (2006) Patents, software and hardware for PID control: an overview and analysis of the current art. IEEE Control Systems Magazine, 26 (1). pp. 42-54. ISSN 0272-1708 (doi:10.1109/MCS.2006.1580153)[永久失效連結]
^ 2.02.12.2 Bennett, Stuart. A history of control engineering, 1930-1955. IET. 1993: p. 48. ISBN 978-0-86341-299-8.
^ Bennett, Stuart. Nicholas Minorsky and the automatic steering of ships (PDF). IEEE Control Systems Magazine. November 1984, 4 (4): 10–15. ISSN 0272-1708. doi:10.1109/MCS.1984.1104827. (原始内容 (PDF)存档于2011-06-08).
^ A Brief Building Automation History. [2011-04-04]. (原始内容存档于2011-07-08).
^ (Bennett 1993,p. 67)
^ Bennett, Stuart. A brief history of automatic control (PDF). IEEE Control Systems Magazine (IEEE). 1996, 16 (3): 17–25.
^ Bennett, Stuart. A history of control engineering, 1800-1930. IET. June 1986: 142–148. ISBN 978-0-86341-047-5.
^ Introduction: PID Controller Design. University of Michigan.
^ Tim Wescott. PID without a PhD (PDF). EE Times-India. October 2000.
^ 10.010.110.2 Ang, K.H., Chong, G.C.Y., and Li, Y. (2005). PID control system analysis, design, and technology, IEEE Trans Control Systems Tech, 13(4), pp.559-576. http://eprints.gla.ac.uk/3817/1/IEEE3.pdf
^ Li, Y., et al. (2004) CAutoCSD - Evolutionary search and optimisation enabled computer automated control system design, Int J Automation and Computing, vol. 1, No. 1, pp. 76-88. ISSN 1751-8520. http://userweb.eng.gla.ac.uk/yun.li/ga_demo/ 页面存档备份,存于互联网档案馆
^ Y Li, KH Ang, GCY Chong, Patents, software, and hardware for PID control: An overview and analysis of the current art, Control Systems, IEEE, 26 (1), 42-54. http://eprints.gla.ac.uk/3816/1/IEEE2pdf.pdf
^ Li, Y. and Ang, K.H. and Chong, G.C.Y. (2006) PID control system analysis and design - Problems, remedies, and future directions. IEEE Control Systems Magazine, 26 (1). pp. 32-41. ISSN 0272-1708
^ Cooper, Douglas. Integral (Reset) Windup, Jacketing Logic and the Velocity PI Form. [2014-02-18].
^ PID and PDFF Compensators for Motion Control (PDF). [2016-10-01]. (原始内容 (PDF)存档于2012-09-01).
^ Cooper, Douglas. PI Control of the Heat Exchanger. Practical Process Control by Control Guru. [2014-02-27].
^ Two-Degree-of-Freedom PID Controllers Mituhiko Araki and Hidefumi Taguchi
^ Discrete PI and PID Controller Design and Analysis for Digital Implementation. Scribd.com. [2011-04-04].
^ 19.019.1 PID process control, a "Cruise Control" example. CodeProject. 2009 [4 November 2012].
Minorsky, Nicolas. Directional stability of automatically steered bodies. J. Amer. Soc. Naval Eng. 1922, 34 (2): 280–309. doi:10.1111/j.1559-3584.1922.tb04958.x.
外部链接
- 改善PID微分和积分的方法及其它控制系统的计算机自动设计CAutoD
- 学习PID和其他系统调试是如何工作的
- PID控制器实验室,PID调试的Java applets
- 一系列的PID调试的Java Applets
- PID调试的问答
- PID控制系统算法的信息和教程
- 用Excel模拟基本的PID
如果用电子部件制作一个PID控制器查看22页- 关于PID控制器的文章,教材
- 一个控制系统的一部分
- PID定速控制應用
- PID馬達定速與定角控制公式比較
- Ang, K.H., Chong, G.C.Y., and Li, Y. (2005), PID control system analysis, design, and technology. IEEE Transactions on Control Systems Technology, 13 (4). pp. 559-576. ISSN 1063-6536
- Understanding Servo Tune(其中包括PID調整方法範例)
- LabView360技術文章 PID
| ||||||||||||||||||||||||||





















![u(t_{k})=u(t_{{k-1}})+K_{p}left[left(1+{dfrac {Delta t}{T_{i}}}+{dfrac {T_{d}}{Delta t}}right)e(t_{k})+left(-1-{dfrac {2T_{d}}{Delta t}}right)e(t_{{k-1}})+{dfrac {T_{d}}{Delta t}}e(t_{{k-2}})right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e71fa41e1c58fcef6f2a3a4118577458ce29c659)
