Cfxtrjtrk

電子

克魯克斯管實驗可以顯示出電子的粒子性質。如圖所示，從左往右直線移動的電子束，遇到一個十字形標靶，從而在真空管右面底端顯示出十字形陰影。
组成	基本粒子
系	費米子
代	第一代
基本相互作用	引力，電磁力，弱核力
符号	e−
反粒子	正電子
发现	约瑟夫·汤姆孙（1897年）
质量	9.109 383 56(11)×10-31 kg[1] 5.485 799 090 70(16)×10-4 amu[1] 0.510 998 9461(31) MeV/c2[1]
平均寿命	穩定
电荷	−1 e[註 1] -1.602 176 6208（98）×10-19 C[1]
磁矩	−1.001 159 652 180 91(26) μB[1]
自旋	1⁄2

电子是一种带有负电的次原子粒子，通常标记为 e−{displaystyle e^{-},!}。電子屬於轻子类，以重力、電磁力和弱核力與其它粒子相互作用。轻子是构成物质的基本粒子之一，无法被分解为更小的粒子。电子带有1/2自旋，是一种费米子。因此，根據泡利不相容原理，任何兩個電子都不能處於同樣的狀態。电子的反粒子是正电子（又称正子），其质量、自旋、帶电量大小都与电子相同，但是电量正負性与电子相反。電子與正子會因碰撞而互相湮滅，在這過程中，生成一對以上的光子。

由电子與中子、质子所组成的原子，是物质的基本单位。相对于中子和质子所組成的原子核，电子的质量显得极小。质子的质量大约是电子质量的1836倍。当原子的电子数与质子数不等时，原子会带电；称該帶電原子为离子。当原子得到额外的电子时，它带有负电，叫阴离子，失去电子时，它带有正电，叫阳离子。若物体带有的电子多于或少于原子核的电量，导致正负电量不平衡时，称该物体带静电。当正负电量平衡时，称物体的电性为电中性。靜電在日常生活中有很多用途，例如，靜電油漆系統能夠將瓷漆（英语：enamel paint）或聚氨酯漆，均勻地噴灑於物品表面。

電子與質子之間的吸引性庫侖力，使得電子被束縛於原子，稱此電子為束縛電子。兩個以上的原子，會交換或分享它們的束縛電子，這是化學鍵的主要成因。当电子脱离原子核的束缚，能够自由移动时，則改稱此電子为自由电子。许多自由电子一起移动所产生的净流动现象称为电流。在許多物理現象裏，像電傳導、磁性或熱傳導，電子都扮演了機要的角色。移動的電子會產生磁場，也會被外磁場偏轉。呈加速度運動的電子會發射電磁輻射。

根據大爆炸理論，宇宙現存的電子大部份都是生成於大爆炸事件。但也有一小部份是因為放射性物質的β衰變或高能量碰撞而生成的。例如，當宇宙線進入大氣層時遇到的碰撞。在另一方面，許多電子會因為與正子相碰撞而互相湮滅，或者，會在恆星內部製造新原子核的恆星核合成過程中被吸收。

在實驗室裏，精密的尖端儀器，像四極離子阱，可以長時間局限電子，以供觀察和測量。大型托卡馬克設施，像国际热核聚变实验反应堆，藉著局限電子和離子電漿，來實現受控核融合。無線電望遠鏡可以用來偵測外太空的電子電漿。

電子被广泛應用于電子束焊接、陰極射線管、電子顯微鏡、放射線治療、激光和粒子加速器等领域。

历史

電現象

大约2500年前，古希臘哲學家泰勒斯已经發現用絲綢或法蘭絨摩擦琥珀（古希臘語：ήλεκτρον ，"ēlektron"）能吸引轻小物体。“electric（電）”這個詞就是起源於希臘語中的“ελεκτρον（琥珀）”^[2]。

東漢時期（約公元一世紀），王充所著書籍《論衡》中有關於靜電的記載^[3]：「頓牟掇芥」。頓牟就是琥珀，當琥珀經摩擦後，即能吸引像草芥一類的輕小物體。西元三世紀，晉朝張華的《博物志》中也有記載：“今人梳頭，解著衣，有隨梳解結，有光者，亦有吒聲”。這裏記載頭髮因摩擦起電發出的閃光和劈啪之聲^[2]。

生於十八世紀，富蘭克林對於電學貢獻良多。

查爾斯·篤費（英语：Charles Du Fay）主張，大自然有兩種不同的「電流體」（electric fluid），它們分別為玻璃電（英语：vitreous electricity）（正電）與樹脂電（英语：resinous electricity）（負電），摩擦的動作可以將它們分離， 合併後會相互中和對方。這理論稱為「雙流體理論」^[4]。稍後，美國科學家埃柏奈澤·肯納斯理（英语：Ebenezer Kinnersley）也獨立獲得相同的結論^[5]:118。

美国人本杰明·富兰克林意识到闪电与摩擦起電涉及到相同的自然要素——後來稱之為電，并且做风筝实验证实這一观點。如同那个時期的大多數科學家，富兰克林认为，電效應是一種瀰漫於所有物體內部的奧妙流體所產生的作用。假设经过某种程序，促使物体得到更多這種流體，则称此物体带正电；假设经过另一种程序，促使物体失去這種流體，则称此物体带负电。若这两个物体互相接触到对方，流體会从带正电物体流往带负电物体。流體的这種重新分布规定了电流方向（与後來觀測到的电子流动方向正好相反）。這是一種「單流體理論」^[6]:122-123。

在1838年至1851年期間，英國醫生理查·萊敏（英语：Richard Laming）提議，原子是由核心物質與以同心圓樣式包圍在四周的帶有單位電荷的次原子粒子所組成；精簡地說，他猜想大自然存在帶有單位電荷的次原子粒子。^[7]在1846年，德國物理學者威廉·韋伯建議，原子的結構類似行星系統，很多帶正電的次原子粒子環繞著一個帶負電的核心物質轉動，次原子粒子的質量非常微小，核心物質的質量非常大。^[8]1874年，愛爾蘭物理學者喬治·斯桐尼（英语：George stoney）建議，在電解現象裡，大自然揭示了電的確切單一數量，這數量與電所作用的物體的種類無關。他又於1891年提議，將這些基本電量（基本電荷）命名為「electron 」（電子），他還嘗試使用法拉第電解定律來估算其數值^[9]。斯桐尼的電子永久束縛在原子內部，無法被移除，每一個原子的化學鍵都會伴隨著電子。這些電子的震動造成周圍乙太的電磁應力。1881年，德國物理學者赫爾曼·馮·亥姆霍茲強調，從法拉第電解定律的結果可以總結，不論是正電或是負電，它們都可被分割為確切的基本單位，其物理行具有粒子性質
^[10]:70-74。

阴极射线

電子束被磁場偏轉成圓形。^[11]

德国物理學者尤利烏斯·普吕克研究蓋斯勒管（英语：Geissler tube）內的稀薄氣體裡的放電現象。他在1858年發現，假設使用白金為陰極的材料，則會有小粒子從陰極剝離。他猜想，剝離的白金粒子因白熾而發出輝光（英语：glow discharge）。他還觀測到，在放電時，在陰極附近的玻璃管壁會出現磷光，其位置會隨著磁場而改變^[12]:392-394。普吕克的學生約翰·希托夫（英语：Johann Hittorf）於1869年進一步發現，假設在陰極與磷光之間置入一個物體，則輝光會被限制在陰極與物體之間，玻璃管壁會因為物體的遮擋而在磷光曲面內出現一塊陰影，這意味著輝光不會轉彎，只會以直線傳播。1876年，德国物理學者歐根·戈爾德斯坦將希托夫的實驗加以擴展，他使用面積較大的陰極，而不是希托夫的點陰極，他發現，輝光的光線並不是朝著所有方向發射，而是朝著垂直於表面的方向發射。他將輝光的光線命名为阴极射线。陰極射線的發射方式與燭光不同，這是一個很大的區別，但希托夫與戈爾德斯坦仍舊認為，陰極射線是某種傳播於乙太的電磁波。儘管如此，他們的研究成果已為未來關於陰極射線本質的辯論撒下了種子。^[13]:55-57

英国人威廉·克鲁克斯在1878年利用一种水银真空泵，制造出了气体含量仅为盖斯勒管1/75000的真空管，被称作克鲁克斯管。克鲁克斯注意到，当逐渐抽出克鲁克斯管内的气体时，阴极附近开始出现黑暗区域，随着真空度的增加，这黑暗区域也会扩张。克鲁克斯提議，这黑暗區域的寬度与阴极粒子的平均自由程有关；黑暗区域与辉光区域的界面，即为粒子与气体分子相互碰撞的起始面；在黑暗区域内，沒有什麼碰撞；而在辉光区域，發生了很多碰撞事件；在管面的螢光，則是因為粒子與管面發生碰撞^[12]:394-395。

克鲁克斯等英国物理学家认为阴极射线并不是射线，而是一种带电粒子。这观点遭到了以海因里希·赫茲为首的德国物理学家的反对^[14]。赫兹的学生德国物理学家菲利普·萊納德在1889年进行了一个实验：他在阳极安装了薄铝箔窗，这样就能把阴极射线导出到空气中。赫兹提出，阴极射线能够穿过薄金属箔，因此它不可能是粒子^[15]。同时，赫兹还在真空管的两侧施加了电场，结果发现并没有观察到预期的偏转，这更加坚定了他的信念。^[16]

發現電子

約瑟夫·湯姆森，電子的發現者。

1895年，讓·佩蘭发现阴极射线能够使真空管中的金属物体带上负电荷，支持了克鲁克斯的理论。1897年，剑桥大学卡文迪许实验室的约瑟夫·汤姆孙重做了赫兹的实验。使用真空度更高的真空管和更强的电场，他观察出阴极射线的偏转，并计算出了阴极射线粒子（电子）的電荷質量比，因此获得了1906年的诺贝尔物理学奖^[17]。汤姆孙採用1891年乔治·斯托尼（英语：George Johnstone Stoney）所起的名字——电子来称呼这种粒子。至此，电子作为人类发现的第一个亚原子粒子和打开原子世界的大门被汤姆孙發现了。^[16]

於1896年，在研究天然發螢光礦石的時候，法國物理學家亨利·貝克勒發現，不需要施加外能源，這些礦石就會自然地發射輻射。這些放射性物質引起許多科學家的興趣，包括發現這些放射性物質會發射粒子的紐西蘭物理學家歐尼斯特·拉塞福。按照這些粒子穿透物質的能力，拉塞福替這些粒子分別取名為阿伐粒子和貝他粒子（「阿伐」是希臘字母的第一個字母「α」，「貝他」是第二個字母「β」）。於1900年，貝克勒發現，鐳元素發射出的貝他射線，會被電場偏轉；還有，貝他射線和陰極射線都有同樣的電荷質量比。這些證據使得物理學家更強烈地認為電子本是原子的一部分，貝他射線就是陰極射線^[12]:408-410。

於1909年，美國物理學家羅伯特·密立根做了一個著名實驗，稱為油滴實驗，可以準確地測量出電子的帶電量。在這實驗裏，他使用電場的庫侖力來抵銷帶電油滴所感受到的重力。從電場強度，他計算出油滴的帶電量。他的儀器可以準確地測量出含有1到150個離子的油滴的帶電量，而且實驗誤差可以限制到低於0.3%。他發現每一顆油滴的帶電量都是同一常數的倍數，因此，他推論這常數必是電子的帶電量。汤姆孙和學生約翰·湯森德（英语：John Townsend）使用電解的離子氣體來將過飽和水蒸氣凝結，經過測量帶電水珠粒的帶電量，他们也得到了相似結果^[13]。於1911年，亞伯蘭·約費（英语：Abram Ioffe）使用帶電金屬微粒，獨立地得到同樣的結果^[18]。但是，油滴比水滴更穩定，油滴的蒸發率較低，比較適合更持久的精準實驗^[19]。

二十世紀初，實驗者發現，快速移動的帶電粒子會在經過的路徑，使過冷卻、過飽和的水蒸氣凝結成小霧珠。於1911年，查爾斯·威爾森應用這理論設計出雲室儀器。這奇妙的發明使得實驗者能夠用照相機拍攝到快速移動電子的軌道，成為早期研究基本粒子的重要方法^[20]。

原子理論

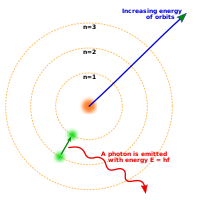
原子的波耳模型示意圖，顯示出以主量子數 n{displaystyle n,!} 標記的三個量子態能級。當一個電子從能級較高的量子態，躍遷至能級較低的量子態時，會發射一個光子；這光子的能量等於兩個量子態的能級差額。

在不同的时代，人们对电子在原子中的存在方式有过各种不同的推测。

最早的原子模型是湯姆森的梅子布丁模型。發表於1904年，湯姆森认为电子在原子中均匀排列，就像帶正電布丁中的帶負電梅子一样^[21]。1909年，著名的拉塞福散射實驗徹底地推翻了這模型^[22]。

拉塞福根據他的實驗結果，於1911年，設計出拉塞福模型。在這模型裏，原子的绝大部分质量都集中於小小的原子核，原子的绝大部分都是真空。而电子则像行星围绕太阳运转一样围绕着原子核运转^[22]。

在经典力学的框架之下，行星轨道模型有一个严重的问题不能解释：呈加速度运动的电子会产生电磁波，而产生电磁波就要消耗能量；最终，耗盡能量的电子将会一头撞上原子核（就像能量耗尽的人造卫星最终会进入地球大气层）。於1913年，尼爾斯·波耳提出了波耳模型。在这模型中，电子运动於原子的某一特定的轨域。距离原子核越远，轨域的能量就越高。當电子從距离原子核更遠的轨域，跃迁到距离原子核更近的轨域时，会以光子的形式釋放出能量。相反的，从低能級轨域跃迁到高能級轨域则會吸收能量。藉著這些量子化轨域，波耳正確地計算出氫原子光譜^[23]。但是，使用波耳模型，並不能夠解釋譜線的相對強度，也無法計算出更複雜原子的光譜^[24]。這些難題，尚待後來量子力學的解釋。

1916年，美國物理化學家吉爾伯特·路易斯成功地解釋了原子與原子之間的相互作用。他建議兩個原子之間一對共用的電子，稱為電子對，形成了共價鍵^[25]。於1923年，瓦尔特·海特勒和弗里茨·伦敦應用量子力學理論，完整地解釋清楚電子對產生和化學鍵形成的原因^[26]。於1919年，歐文·朗繆爾將路易斯的立方原子模型（英语：cubical atom）加以發揮，建議所有電子都分佈於一層層同心的（接近同心的）、等厚度的球形殼。他又將這些球形殼分為幾個部分，每一個部分都含有一對電子。使用這模型，他能夠解釋週期表內每一個元素的週期性化學性質^[27][28]。

1924年，奧地利物理學家沃爾夫岡·包立用一組參數來解釋原子的殼層結構。這一組的四個參數，決定了電子的量子態。每一個量子態只能容許一個電子佔有。（這禁止多於一個電子佔有同樣的量子態的規則，稱為泡利不相容原理）。這一組參數的前三個參數分別為主量子數、角量子數和磁量子數。第四個參數只能有兩種選擇。於1925年，荷蘭物理學家塞缪尔·古德斯米特和喬治·烏倫貝克提出了第四個參數所代表的物理機制。他們認為電子，除了運動軌域的角動量以外，可能會擁有內在的角動量，稱為自旋；這性質可以用來解釋先前在實驗裡，用高解析度光譜儀觀測到的神秘的精細結構分裂，即原子譜線從先前的一條線分裂成數條線^[29]。

量子力學

1924年，法國物理學家路易·德布羅意在他的博士論文《量子理论研究》（《Recherches sur la théorie des quanta》）裏，提出了德布羅意假說，假設所有物質都擁有類似光波的波動性質^[30]。按照這假設，給予適當的條件，電子和其它物質會顯示出波動的性質。假若，物理實驗能夠顯示出，隨著時間演化，物體移動於空間軌道的局域位置，則這實驗明確地顯示了粒子性質。假若，物理實驗能夠顯示出，粒子通過狹縫後，會產生干涉圖樣於偵測屏障，則這實驗明確地顯示了波動性質。1927年，英國物理學家喬治·湯姆森用金屬薄膜，美國物理學家柯林頓·戴維森和雷斯特·革末用鎳晶體，分別將電子的干涉效應顯示於偵測屏障^[31]。

在量子力學裏，束縛於原子內部的電子的物理行為可以用原子軌域來描述，這軌域並不是軌道，而是機率幅。機率分佈是機率幅絕對值的平方。此圖顯示1s原子軌域。某位置的色彩濃淡表示電子處於那位置的相對機率。

德布羅意的博士論文給予埃爾溫·薛丁格莫大的啟示：既然粒子具有波動性，那必定有一個波動方程式，能夠完全地描述這粒子的波動行為。1926年，薛丁格提出了薛丁格方程式。這波動方程式能夠描述電子的波動行為^[32]。它並不能命定性地給出電子的明確運動軌道，電子在任意時間的位置。但是，它可以計算出電子處於某位置的機率，也就是說，在某位置找到電子的機率。薛定諤用自己想出的方程式來計算氫原子的譜線，得到了與用波耳模型的預測雷同的答案。再進一步將電子的自旋和幾個電子的互相作用納入考量，薛丁格方程式也能夠給出電子在其它原子序較高的原子內的電子組態^[33]。

1928年，保羅·狄拉克發表了狄拉克方程式。這公式能夠描述相對論性電子的物理行為^[34]。相對論性電子是移動速度接近光速的電子。為了要解釋狄拉克方程式的自由電子解所遇到的反常的負能量態問題，狄拉克提出了一個真空模型，稱為狄拉克之海，即真空是擠滿了具有負能量的粒子的無限海。因此，他預言宇宙中存在有正子（電子的反物質搭配）^[35]。1932年，卡爾·安德森在宇宙射線實驗中首先證實了正子的存在^[36]。

1947年，威利斯·蘭姆在與研究生羅伯特·雷瑟福（Robert Retherford）合作的實驗中，發現氫原子的某些應該不會有能量差值的簡併態，竟然出現很小的能量差值。這現象稱為蘭姆位移。大約同年代，波利卡普·庫施和亨利·福立（英语：Henry Foley）在共同完成的一個實驗中，發現電子的異常磁矩，即電子的磁矩比狄拉克理論的預估稍微大一點。為了解釋這些現象，朝永振一郎、朱利安·施溫格和理察·費曼，於1940年代，創建了量子電動力學^[37]。

粒子加速器

二十世紀的前半世紀，粒子加速器運作所需的理論與設備都已發展成熟。物理學家已經準備好更進一步地研究亞原子粒子的性質^[38]。1942年，唐納德·克斯特（英语：Donald Kerst）首先成功地使用電磁感應將電子加速至高能量。在他領導下，貝他加速器最初的能量達到2.3百万电子伏（MeV）；後來，能量更達到300MeV。1947年，在通用電器實驗室，使用一台70MeV電子同步加速器，物理學家發現了同步輻射，即移動於磁場的相對論性電子因為加速度而發射的輻射^[39]。

1968年，第一座粒子束能量高達1.5吉电子伏（GeV），名為大儲存環對撞機（英语：ADONE）的粒子對撞機（英语：particle collider），在義大利的核子物理國家研究院（英语：Istituto Nazionale di Fisica Nucleare）開始運作。這座對撞機能夠將電子和正子反方向地分別加速。與用電子碰撞一個靜止標靶相比較，這方法能夠有效地使碰撞能量增加一倍^[40]。從1989年運行到2000年，位於瑞士日內瓦近郊的歐洲核子研究組織的大型電子正子對撞機，能夠實現高達209GeV的碰撞能量。這對撞機曾經完成多項實驗，對於考練與核對粒子物理學的標準模型的正確性有很大的貢獻^[41]。

物理特性

分類

基本粒子的標準模型。電子位於左下方。

在粒子物理學裏，根據標準模型，電子屬於亞原子粒子中的輕子類。電子是基本粒子。在所有帶電的輕子中，電子的質量最小，屬於第一代基本粒子^[42]。緲子和陶子分別為第二代和第三代的輕子。它們的電荷量、自旋和基本交互作用，都與電子相同；質量都大於電子。輕子與夸克的主要不同點是輕子不以強核力與其它粒子相互作用^[43]。輕子的自旋是半奇數。凡是自旋為半奇數的粒子都是費米子。所以，輕子是費米子^[44]。電子的自旋是 1/2{displaystyle 1/2,!}^[45]。

基本性質

電子的質量大約為9.109 × 10⁻³¹公斤或5.489 × 10⁻⁴amu^[1]。根據阿爾伯特·愛因斯坦的質能等價原理，這質量等價於0.511 MeV靜止能量。質子質量大約為電子質量的1836倍^[46]。天文測量顯示出，至少在最近這半個宇宙的年齡期間，這質量比例都保持穩定不變，就如同標準模型所預測的一樣^[47]。

電子帶有的電量是基本電荷電量：-1.602 × 10⁻¹⁹庫侖^[1]，這是亞原子粒子所使用的電荷單位的電量。在實驗準確極限內，電子的絕對帶電量與質子相等，但正負號相反^[48]。基本電荷通常用符號 e{displaystyle e,!} 表示。電子用符號 e−{displaystyle e^{-},!} 表示；正子用符號 e+{displaystyle e^{+},!} 表示^[1]；其中，正負號分別表示帶有正負電荷。除了帶有電荷的正負號不同以外，正子與電子的其它性質都相同^[49]:21。

電子擁有內在的角動量，稱為自旋。電子的自旋量子數為 s=1/2{displaystyle s=1/2,!}。通常，當談到這性質時，電子會被指為是一種自旋1/2粒子。對於這種粒子，自旋角動量是 3ℏ/2{displaystyle {sqrt {3}}hbar /2,!}^{[註 2]}。
任何有關自旋的射影於任意坐標軸的測量，得到的答案只能為 ±ℏ/2{displaystyle pm hbar /2,!}。沿著自旋軸，電子的內在磁矩大約為1波耳磁元，或9.274 009 15（23）×10⁻²⁴焦耳/特斯拉^[1]。電子的自旋對於動量方向的投影為電子的螺旋度^[49]:137-138。

電子沒有任何次結構^[50]。物理學家認為電子是一個點粒子，不占有任何空間^[51]。從觀測束縛於潘寧阱內的電子而得到的實驗結果，物理學家推斷電子半徑的上限為10⁻²²公尺^[52]。古典電子半徑（英语：classical electron radius）是2.8179 × 10⁻¹⁵米。這個結果是從古典電動力學和狹義相對論的理論推論出來的，並沒有使用到任何量子力學理論
^{[註 3]}。

很多基本粒子會自發衰變成質量更輕的粒子，緲子就是一個很好的例子。平均壽命為2.2 × 10⁻⁶秒的緲子會衰變成一個電子、一個微中子和一個反微中子。從现有理論論證，電子是很穩定的：電子是質量最輕的帶電粒子，它的衰變會違反電荷守恆定律。電子平均壽命的實驗最低限是4.6 × 10²⁶年，信賴區間是90%^[53]。

量子性質

在雙縫實驗裏，通過兩條狹縫，抵達偵測屏障的電子，一顆顆地累積，顯示出干涉圖樣。^{[註 4]}

如同所有其它粒子，電子具有粒子性和波動性。這性質稱為波粒二象性。在雙縫實驗裏，電子的波動性質，使得通過兩條狹縫的電子波互相干涉，造成了顯示於偵測屏障的明亮條紋和黑暗條紋，這就是如左圖所示雙縫實驗特徵的干涉圖樣。使用更高階的實驗設備，可以觀測到，電子總是以一顆顆粒子的方式抵達偵測屏障^{[55][註 4]}。電子的波動行為可以用複值的含時波函數 ψ{displaystyle psi ,!} 來描述。波函數在某位置 r{displaystyle mathbf {r} ,!} 與時間 t{displaystyle t,!} 的值 ψ(r,t){displaystyle psi (mathbf {r} ,,t),!}，稱為量子幅。電子在時間 t{displaystyle t,!} 處於位置 r{displaystyle mathbf {r} ,!} 的機率密度是量子幅絕對值的平方 |ψ(r,t)|2{displaystyle |psi (mathbf {r} ,,t)|^{2},!}。^{[註 5]}

在無限深方形阱裏，兩個全同費米子的反對稱性波函數繪圖。^{[註 6]}

給定兩個粒子的波函數分別為 ψa{displaystyle psi _{a}}、ψb{displaystyle psi _{b}}。假若這兩個粒子可以被區分，那應該可以確定哪個波函數描述的是第一個粒子，哪個波函數描述的是第二個粒子。假若 ψa{displaystyle psi _{a}} 描述的是第一個粒子，ψb{displaystyle psi _{b}} 描述的是第二個粒子，則這兩個粒子的總波函数可以表示為 ψa{displaystyle psi _{a}}、ψb{displaystyle psi _{b}} 的簡單乘積：

ψ(1,2)=ψa(1)ψb(2){displaystyle psi (1,2)=psi _{a}(1)psi _{b}(2)}。

否則，假若 ψb{displaystyle psi _{b}} 描述的是第一個粒子，ψa{displaystyle psi _{a}} 描述的是第二個粒子，這兩個粒子的總波函数可以表示為

ψ(1,2)=ψb(1)ψa(2){displaystyle psi (1,2)=psi _{b}(1)psi _{a}(2)}。

現在假設這兩個粒子是全同粒子，不可以區分到底哪個粒子是第一個粒子，哪個粒子是第二個粒子。這意味著波函數 ψa{displaystyle psi _{a}} 可能描述的是第一個粒子，也有可能描述的第二個粒子。同樣地波函數 ψb{displaystyle psi _{b}} 可能描述的是第一個粒子，也有可能描述的第二個粒子。這兩個粒子量子行為的機率對於粒子交換應該具有不變性：

|ψ(1,2)|2=|ψ(2,1)|2{displaystyle |psi (1,2)|^{2}=|psi (2,1)|^{2}}。

只有兩種總波函數的形式可以獲得這結果方法。一種是對稱性總波函數：^[49]:181-188

ψ(1,2)=C[ψa(1)ψb(2)+ψa(2)ψb(1)]{displaystyle psi (1,2)=C[psi _{a}(1)psi _{b}(2)+psi _{a}(2)psi _{b}(1)]}；

其中，C{displaystyle C} 是歸一化常數，與 ψa{displaystyle psi _{a}}、ψb{displaystyle psi _{b}} 有關。

另一種是反對稱性總波函數：

ψ(1,2)=[ψa(1)ψb(2)−ψa(2)ψb(1)]/2{displaystyle psi (1,2)=[psi _{a}(1)psi _{b}(2)-psi _{a}(2)psi _{b}(1)]/{sqrt {2}}}。

從反對稱性總波函數的形式可以推論，假設兩個全同粒子的波函数對於粒子交換具有反对称性，並且它們佔有同一量子態，即它們的波函數相同，

ψa=ψb{displaystyle psi _{a}=psi _{b}}，

則總波函數等於零：

ψ(1,2)=[ψa(1)ψa(2)−ψa(2)ψa(1)]/2=0{displaystyle psi (1,2)=[psi _{a}(1)psi _{a}(2)-psi _{a}(2)psi _{a}(1)]/{sqrt {2}}=0}。

費米子的自旋為半整數，總波函數對於粒子交換具有反對稱性。因此，泡利不相容原理表明，两个全同费米子在同一个系统中永远无法占据同一量子态。並沒有涉及到任何位勢，並沒有任何作用力施加於它們本體，這純粹是從無法區分全同粒子而產生的一種量子性質，在經典物理學裏，找不到類似性質。^[56]:201-210

電子是全同費米子。沒有任何方法能夠分辨出一個電子與另一個電子有甚麼不同；沒有任何方法能夠區分出，在一群電子之中，哪一個電子是哪一個電子。遵循泡利不相容原理，任意兩個電子都不能佔有同樣的量子態。這原理解釋了許多有關電子在原子內的性質。例如，在原子內，一個原子軌域裏，最多只能有兩個束縛電子，為了符合反對稱性，一個電子的自旋往上，另一個電子的自旋往下；而不是所有的束縛電子都佔有同樣一個最低能級的軌域。^[56]:210-214

虛粒子

物理學家認為，空間會繼續不停地生成一對一對的虛粒子，像正子-電子虛偶，而在生存短暫的一段時間後，這些成對的虛粒子會互相摧毀對方^[57]。在這過程裏，生成虛粒子所需要的能量漲落 ΔE{displaystyle Delta E,!}，虛粒子能夠被偵測所需要的存在時間 Δt{displaystyle Delta t,!}，都綜合地表達於海森堡不確定原理所設定的偵測底限，ΔEΔt≥ℏ{displaystyle Delta EDelta tgeq hbar ,!}；其中，ℏ{displaystyle hbar ,!} 是約化普朗克常數。實際而言，生成這些虛粒子所需要的能量 ΔE{displaystyle Delta E,!}，可以從真空暫時借用一段時間 Δt{displaystyle Delta t,!}，只要它們的乘積小於約化普朗克常數 ℏ{displaystyle hbar ,!} 就行。這樣，理論上不會被儀器偵測出來，也不會違反海森堡不確定原理。根據這推理，對於虛電子，Δt{displaystyle Delta t,!} 最多是1.3 × 10⁻²¹秒^{[註 7]}。

略圖顯示電子-正子虛偶的隨機性地出現於一個電子（左下方）的附近。

如左圖所示，電子-正子虛偶會隨機性地出現於一個電子（圖內左下方）的附近。當電子-正子虛偶尚然存在的時候，新生成的正子，會感受到原本電子施加的吸引性庫侖力；而新電子則會感受到排斥性庫侖力。這現象稱為真空極化。真空變得好像一個具有電容率 ϵ>1{displaystyle epsilon >1,!} 的電介質。因此，電子的有效電荷量變得小於真實值量，而且隨著離原本電子距離的增加而遞減^[58]。通过1997年用日本崔斯坦粒子加速器（英语：KEKB (accelerator)）所做的實驗，真空極化理論得到了强有力的證實^[59]。對於電子的質量，虛粒子也會造成屏蔽效應^[60]。

虛粒子交互作用能夠解釋，在電子的內在磁矩與波耳磁元之間，微小的偏差（大約是磁矩的0.1%），稱為異常磁矩^[61]。這理論結果超特準確地與實驗測定的數值相符合。無可否認地，在這裡，量子電動力學交出了一份漂亮的成績單^[62]。

在經典物理裏，一個物體的角動量和磁矩跟其物理尺寸有關。因此，無尺寸電子擁有這些性質的概念實在令人百思。一個可能合理的解釋為，在電子本身所產生的電場，能夠生成虛光子。這些虛光子促使電子快速地震顫，稱為顫動，因而造成電子的進動。經過過濾掉漲落後，淨運動是圓周運動。這奇特的運動造成了電子的自旋和磁矩^[51][63]。在原子裏，做譜線實驗觀察到的蘭姆位移，可以用虛光子生成的理論來解釋^[58]。

相互作用

帶有電量 q{displaystyle q} 的粒子以速度 v{displaystyle mathbf {v} } 移動於磁場 B{displaystyle mathbf {B} } （磁場的方向是從銀幕指向眼睛），該粒子因感受到勞侖茲力的作用而呈現出的可能運動軌道。

電子是帶負電粒子，其所產生的電場，會吸引像質子一類的帶正電粒子，也會排斥像電子一類的帶負電粒子，這些現象所涉及的作用力遵守庫侖定律^[64]:58-61。一群電子在空間中移動的動作會形成電流，安培定律描述電流與電流所產生的磁場彼此之間的關係^[64]:225-236。這種感應性質給出了驅動電動機的磁場^[65]:134。

根據經典電動力學，一個任意移動的帶電粒子，必須經過一段傳播時間，才能夠將其影響傳播到場位置，在場位置產生對應的推遲勢，稱為黎納-維謝勢^[64]:429-434。這一段時間的長短跟帶電粒子位置、場位置之間的距離有關。任意移動的帶電粒子所產生的電場和磁場，可以從黎納-維謝勢求得，也可以用傑斐緬柯方程式直接計算出來^[64]:427-429。應用狹義相對論，也可以推導出同樣的結果^[64]:525-532。

移動於磁場的電子，會感受到勞侖茲力的作用。這勞侖茲力垂直於磁場與電子速度兩個向量所決定的平面，是向心力，促使電子按照螺旋軌道移動於磁場。螺旋軌道的半徑稱為迴轉半徑。由於螺旋運動涉及加速度，電子會發射電磁輻射。對於這過程，非相對論性電子發射的電磁輻射稱為迴旋輻射；而相對論性電子發射的則稱為同步輻射^[66]。發射電磁輻射的同時，電子也會感受到一種反衝力，稱為阿布拉罕-勞侖茲-狄拉克力，使得電子的移動速度減緩。阿布拉罕-勞侖茲-狄拉克力，是由電子自身產生的電磁場，施加於自己本身的作用力^[67]。

費曼圖表示電子感受到由光子傳遞的電磁交互作用。

在量子電動力學裏，粒子與粒子之間傳遞電磁交互作用的玻色子是光子。一個不呈加速度運動的孤獨電子，是無法發射或吸收真實光子的。因為，這樣做會違背能量守恆定律和動量守恆定律。然而，虛光子不須遵守這禁忌。虛光子可以擔當傳輸動量於兩個帶電粒子之間的責任。例如，兩個帶電粒子互相交換虛光子這動作，形成了庫侖力^[68]。假設，一個移動中的電子，感受到一個帶電粒子（像質子）所產生的電場的庫侖力，而產生偏轉（英语：deflection (physics)），則電子會因為加速度運動而發射電磁輻射，這稱為轫致辐射
^[69]。

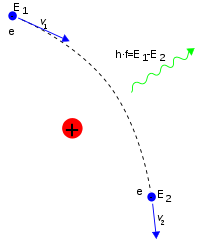
一個電子移動於原子核所產生的電場，會被電場的庫侖力偏轉，因而發射轫致辐射。電子的能量的改變 E2−E1{displaystyle E_{2}-E_{1}}，決定了發射光子的頻率。

康普頓散射是光子與自由電子之間的彈性碰撞。這種碰撞涉及動量和能量的傳輸於兩個粒子之間，會改變光子的波長。改變的波長差值稱為康普頓位移^{[註 8]}。這差值的最大值，稱為康普頓波長^[70]，以方程式表達為 h/mec{displaystyle h/m_{e}c}；其中，h{displaystyle h} 是普朗克常數，me{displaystyle m_{e}} 是電子質量，c{displaystyle c} 是光速。電子的康普頓波長為2.43 × 10⁻¹² m^[1]。對於長波長的光波（例如，可見光的波長域為0.4–0.7 μm），康普頓波長會顯得相當微小，稱這種散射為湯姆森散射。

當電子與正子相互碰撞時，它們會互相湮滅對方，同時生成兩個以上，偶數的伽馬射線光子，以180°相對角度發射出去。假若，可以忽略電子和正子的動量，則這碰撞可能會先形成正子電子偶原子，然後再湮滅成為兩個0.511 MeV伽馬射線光子。^[71][72]

逆反過來，高能量光子可以轉變為一個電子和一個正子，這程序稱為成對產生。但是，由於違背了動量守恆定律，單獨光子不可能會發生成對產生。只有在像原子核等等的帶電粒子附近，由於庫侖作用，能量大於1.022 MeV的光子才有可能發生成對產生^[73]。

費曼圖表示電子感受到由W玻色子或Z玻色子傳遞的弱交互作用。

輕子的量子態是由遵守狄拉克方程式的狄拉克旋量來表達。狄拉克旋量有四個複值分量，可以用投影算符按照手徵性分為左手部分與右手部分。根據弱交互作用理論，電子狄拉克旋量的左手部分會與電微中子狄拉克旋量形成弱同位旋二重態。對於弱交互作用，電微中子的物理行為有點類似電子。二重態的任何一個成員，都可以發射或吸收一個W玻色子，從而轉變為另為一個成員。這過程稱為電性流交互作用。W玻色子帶有一個單位電荷，這抵消了在遷變時，任何淨電量變化，這過程遵守電荷守恆定律。放射性原子的貝他衰變現象所涉及的就是電性流交互作用。電子和電微中子可以互相交換Z玻色子，這過程稱為中性流交互作用，微中子-電子彈性散射（英语：elastic scattering）所涉及的就是中性流交互作用。^[74]

原子和分子

原子內部有一個原子核與一群被原子核束縛的電子。由於庫侖力的作用，原子內的電子被原子核吸引與束縛。假若，束縛電子的數目不等於原子核的質子數目，則稱此原子為離子。在原子內，原子軌域描述束縛電子的物理行為。每一個原子軌域都有自己獨特的一組離散的量子數，像主量子數、角量子數和磁量子數。對於原子軌域，主量子數設定能級，角量子數給出軌角動量，而磁量子數則是軌角動量對於某特定軸的（量子化的）投影。根據泡利不相容原理，每一個原子軌域只能被兩個電子佔據，而這兩個電子必須有反對稱的的自旋波函數，一個自旋向上，另一個自旋向下^[56]:214-217。

電子的機率密度繪圖。橫排顯示不同的角量子數 ℓ{displaystyle ell ,!} ,豎排顯示不同的能級 n{displaystyle n,!}。

處於一個軌域的電子，經過發射或吸收光子的過程，可以躍遷至另外一個軌域。發射或吸收的光子的所涉及的能量必須等於軌域能級的差值。除了這種方法以外，電子也可以藉著與它粒子的碰撞，或靠著俄歇效應，躍遷至別的軌域^[75]。假若，給予束縛電子的能量大於其束縛能，則這束縛電子可以逃離原子，成為自由電子。例如，在光電效應裏，一個能量大於原子電離能的入射光子，被電子吸收，使得電子有足夠的能量逃離原子。^[76]

電子的軌角動量是量子化的。由於電子帶有電荷，其軌磁矩與軌角動量成正比。原子的淨磁矩是原子核與每一個電子的軌磁矩和自旋磁矩的總向量和（欲知道更詳細的資料，請參閱自旋-軌道作用）。但是，與電子的磁矩相比，核磁矩顯得超小，可以忽略。處於同樣軌域的兩個偶電子會互相抵銷對方的自旋磁矩^[77]。

原子與原子之間的化學鍵是因為電磁作用而形成的，這物理行為可以用量子力學理論來描述。幾種常見的化學鍵為離子鍵、共價鍵和金屬鍵。在離子化合物裏，正離子和負離子會通過靜電作用形成離子鍵。在共價化合物裏，原子與原子之間通過共用電子形成共價鍵。在金屬裏，自由電子與排列成晶格狀的金屬離子之間的靜電吸引力形成金屬鍵。分子是由多個原子在共價鍵中透過共用電子連接一起而形成。在分子內部，電子的運動會同時感受到幾個原子核的影響。電子佔有分子軌域，就好像在孤獨原子內部佔有原子軌域一樣。在分子結構裏，一個很重要的因素是電子偶的存在。電子偶是兩個自旋相反的電子組成；遵守泡利不相容原理，這兩個電子共處於同一個分子軌域，就好像處於同一個原子軌域一樣。不同的分子軌域有不同的電子機率密度分佈。例如，共價鍵電子偶（實際連接原子在一起的共價鍵的電子偶）的電子，最常處於原子之間比較小的空間。反過來說，非共價鍵電子偶的電子會分佈於環繞著原子核的比較大的空間^[78]。

電傳導和熱傳導

閃電機制涉及電子或離子從雲層向地面流動或從地面向雲層流動。

假若，一個物體所擁有的電子數量與質子數量不相等，則此物體帶有淨電荷。當電子數量比較多的時候，稱此物體帶有負電；而當電子數量比較少的時候，稱此物體帶有正電；又當電子數量與質子數量相等時，稱此物體為電中性。一個巨觀物體可以通過摩擦而帶有淨電荷，稱此效應為摩擦起電效應。^[79]

移動於真空的獨立電子稱為自由電子。自由電子不束縛於原子內。在金屬內的電子的物理行為好似自由電子。實際而言，這些在金屬內的電子是準電子。更仔細而言，它們是準粒子，所擁有的電荷量、自旋、磁矩，與真實電子的等值；但是有效質量不等值^[80]。當自由電子移動於金屬或真空時，它們會造成電荷的淨流動，稱為電流。載流導線是載有電流的導線。環繞著載流導線的四周，會生成磁場；而隨著時間而改變的磁場，稱為含時磁場，又會生成電流。這些電磁現象的物理行為，可以用馬克士威方程組來描述。^[81]

電導率是表示物質傳輸電流的能力的一種測量值。當施加電壓於導體的兩端時，電子會從低電勢處朝著高電勢處移動，因而產生電流。依照慣例，對於導體，電流的方向與電子移動的方向恰巧相反。銅和金都是優良導體；而玻璃和橡膠則都是不良導體。在電介質裏，電子束縛於各自所屬的原子內，電介質的性質就好像絕緣質一樣。金屬物質擁有電子能帶結構，其電子能帶還沒有完全被電子填滿。這些尚未填滿的電子能帶，容許金屬內一些電子的舉止，好似自由電子或離域電子一般，與任何一個原子都沒有連結。當施加電場於金屬時，這些電子可以自由的移動於金屬，就像氣體移動於其容器內一般，稱這些電子為費米氣體^[56]:218-229。

在導體裏，由於電子與原子之間的碰撞，電子的漂移速度大約為每秒幾公分。但是，在導體內部某位置電子密度的變化，傳達到其它位置的速度，稱為傳播速度，通常大約是光速的75%。這是因為電子訊號的傳播類似光波，傳播速度與物質的相對電容率有關^[82]。

金屬的熱傳導性良好。主要原因是離域電子可以在原子與原子之間自由的傳輸熱能。但是，與電導率不同的是，熱導率幾乎與溫度無關。維德曼-夫蘭茲定律清楚的闡明這關係：熱導率與電導率的比率跟溫度成正比^[83]。金屬晶格因熱能而產生的無序現象，使得物質的電阻率增加，從而造成電導率與溫度有關^[84]。

當降低溫度至低於臨界溫度時，物質會發生相變，從一種相態忽然變成另一種相態。假若在這同時，出現電阻變為零的現象，電流可以毫無損耗的流動於物質，則稱此現象為超導現象。BCS理論是解釋這超導現象的量子理論。BCS理論認為，這量子行為可以用庫珀對模型來解釋。庫珀對是處於玻色-愛因斯坦凝聚量子態的成對的電子；它們的運動，通過晶格的振動（稱為聲子），與鄰近原子耦合，因此避免了與原子碰撞的機會。這樣，就不會有電阻出現了^[85]。高溫超導現象的運作機制與基礎理論仍舊不清楚。

在固態導體內，電子是準粒子。當將溫度嚴格地控制於接近絕對零度時，電子的物理行為變得好像分裂為另外兩個準粒子，旋子和洞子。旋子擁有自旋和磁矩；而洞子則帶有電荷^[86]。

相對論性電子的性質

根據愛因斯坦的狹義相對論，相對於觀測者的參考系，電子的移動速度越快，電子的相對論性質量（總能量）也越大，因而使得電子繼續加速所需要的能量越來越大，在接近光速時，趨向於無窮大。因此電子的移動速度可以接近光波在真空的傳播速度 c{displaystyle c,!}，但絕不會達到 c{displaystyle c,!}^[87]:20-24。

光波傳播於像水一類的電介質的速度 vL{displaystyle v_{L},!}，會明顯地小於 c{displaystyle c,!}。假設，將相對論性電子（電子的速度接近 c{displaystyle c,!} ）入射於這一類的電介質，則相對論性電子在此電介質內的移動速度，會暫時地大於光波傳播於此電介質的速度 vL{displaystyle v_{L},!}。當相對論性電子移動於此類電介質內部時，由於與電介質相互作用，會產生一種很微弱的輻射，稱為契忍可夫輻射^[88]。

勞侖茲因子與速度的關係線圖。當速度超小於 c{displaystyle c,!} 時，勞侖茲因子大約為1，當速度趨向 c{displaystyle c,!} 時，勞侖茲因子趨向無限大。

狹義相對論的效應要視勞侖茲因子的大小而決定。勞侖茲因子 γ{displaystyle gamma ,!} 以方程式定義為

γ=def1/1−v2/c2{displaystyle gamma {stackrel {def}{=}}1/{sqrt {1-v^{2}/c^{2}}},!}；

其中，v{displaystyle v,!} 是粒子的速度。

一個電子的動能 Ke{displaystyle K_{e},!} 是

Ke=(γ−1)mec2{displaystyle K_{e}=(gamma -1)m_{e}c^{2},!}；

其中，me{displaystyle m_{e},!} 是電子的靜質量。

例如，史丹福直線加速器可以將電子加速到大約51 GeV^[89]。由於電子的靜質量大約為0.51 MeV，對應的 γ{displaystyle gamma ,!} 值接近100,000。給予同樣的速度，這電子的相對論性動量 γmev{displaystyle gamma m_{e}v,!} 是經典力學預測的動量 mev{displaystyle m_{e}v,!} 的100,000倍^{[註 9]}。

電子也擁有波動行為，其德布羅意波長 λ{displaystyle lambda ,!} 以方程式表達為 λ=h/p{displaystyle lambda =h/p,!}；其中，h{displaystyle h,!} 是普朗克常數，p{displaystyle p,!} 是動量^[30]。對於前述的51 GeV電子，λ{displaystyle lambda ,!} 大約為2.4 × 10⁻¹⁷，這波長的尺寸相當微小，所以，實驗者可以用電子來精密地探測原子核的內部結構^[90]。

電子天文學理論

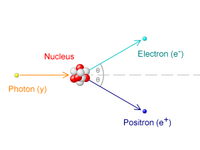
高能量光子能夠與原子核的庫侖場相互作用，從而生成電子和正子。這過程稱為電子正子成對產生。

在眾多解釋宇宙早期演化的理論中，大爆炸理論是比較能夠被物理學界廣泛接受的科學理論^[91]:2。在大爆炸的最初幾秒鐘時間，溫度遠遠高過100億K。那時，光子的平均能量超過1.022 MeV很多，有足夠的能量來生成電子和正子對^{[92]:第2.1.4節}。這過程稱為電子正子成對產生，以公式表達為

γ+γ⇋e++e−{displaystyle gamma +gamma leftrightharpoons mathrm {e} ^{+}+mathrm {e} ^{-},!}；

其中，γ{displaystyle gamma ,!} 是光子，e+{displaystyle mathrm {e} ^{+},!} 是正子，e−{displaystyle mathrm {e} ^{-},!} 是電子。

同時，電子和正子對也在大規模地相互湮滅對方，並且發射高能量光子。在這短暫的宇宙演化階段，電子，正子和光子努力地維持著微妙的平衡。但是，因為宇宙正在快速地膨脹中，溫度持續轉涼，在10秒鐘時候，溫度已降到30億K，低於電子-正子生成過程的溫度底限100億K。因此，光子不再具有足夠的能量來生成電子和正子對，大規模的電子-正子生成事件不再發生。可是，電子和正子還是繼續不段地相互湮滅對方，發射高能量光子^{[92]:第2.1.4節}。由於某些尚未確定的因素，在輕子生成過程（英语：leptogenesis (physics)）中，生成的電子多於正子。否則，假若電子數量與正子數量相等，現在就沒有電子了^{[93]:110-112[94]}！不只這樣，由於一種稱為重子不對稱性的狀況，質子的數目也多過反質子，大約每1億個粒子對與光子中，就會有一個額外的質子^[93]:134。很巧地，電子存留的數目跟質子多過反質子的數目正好相等。因此，宇宙淨電荷量為零，呈電中性^[94]。

假若溫度高於10億K，任何質子和中子結合而形成的重氫，會立刻被高能量光子光解。在大爆炸後100秒鐘，溫度已經低於10億K，質子和中子結合而成的重氫，不再會被高能量光子光解，存留的質子和中子開始互相參予反應，形成各種氫的同位素和氦的同位素，和微量的鋰和鈹。這過程稱為太初核合成^{[92]:第2.1.5節}。

在大約1000秒鐘時，溫度降到低於4億K。核子與核子之間，不再能靠著高速度隨機碰撞的機制，克服庫侖障壁，互相接近，產生核融合。因此，太初核合成過程無法進行，太初核合成階段大致結束^{[92]:第2.1.6節}。任何剩餘的中子，會因為半衰期大約為614秒的負貝他衰變，轉變為質子，同時釋出一個電子和一個反電微中子：

n⇒p+e−+ν¯e{displaystyle mathrm {n} Rightarrow mathrm {p} +mathrm {e} ^{-}+{bar {mathrm {nu } }}_{mathrm {e} },!}；

其中，n{displaystyle mathrm {n} ,!} 代表中子，p+{displaystyle mathrm {p} +,!} 代表質子，ν¯e{displaystyle {bar {mathrm {nu } }}_{mathrm {e} },!} 代表反電微中子。

在以後的377,000年期間，電子的能量仍舊太高，無法與原子核結合。在這時期之後，隨著宇宙逐漸地降溫，原子核開始束縛電子，形成中性的原子。這過程稱為復合。在這相當快的復合過程時期之後，大多數的原子都成為中性，光子不再會很容易地與物質相互作用。光子也可以自由地移動於透明的宇宙^[95]。

大爆炸的一百萬年之後，第一代恆星開始形成^[95]。在恆星內部，恆星核合成過程的各種核融合，會造成正子的生成（參閱質子-質子鏈反應和碳氮氧循環）。這些正子立刻會與電子互相湮滅，同時釋放伽瑪射線。結果是電子數目穩定地遞減，跟中子數目對應地增加。恆星演化過程會合成各種各樣的放射性同位素。有些同位素隨後會經歷負貝他衰變，同時發射出一個電子和一個反電微中子結果是電子數目增加，跟中子數目對應地減少。例如，鈷-60（⁶⁰Co）同位素會因衰變而形成鎳-60^[96]。

質量超過20太陽質量的恆星，在它生命的終點，會經歷到引力坍縮，因而變成一個黑洞^[97]。按照相對論理論，黑洞所具有的超強引力，足可阻止任何物體逃離，甚至電磁輻射也無法逃離。但是，物理學家認為，量子力學效應可能會允許電子和正子生成於黑洞的事件視界，因而使得黑洞發射出霍金輻射，。

當一對虛粒子，像正子-電子虛偶，生成於事件視界或其鄰近區域時，這些虛粒子的隨機空間分佈，可能會使得其中一個虛粒子，出現於事件視界的外部。這過程稱為量子穿隧效應。黑洞的引力勢會供給能量，使得這虛粒子轉變為真實粒子，輻射逃離黑洞。這輻射程序稱為霍金輻射。在另一方面，這程序的代價是，虛偶的另一位成員得到了負能量。這會使得黑洞淨損失一些質能。霍金輻射的發射率與黑洞質量成反比；質量越小，發射率越大。這樣，黑洞會越來越快地蒸發。在最後的0.1秒，超大的發射率可以類比於一個大爆炸^[98]。

高能量宇宙線入射於地球大氣層，造成了一陣持久的空中射叢。

宇宙線是遨遊於太空的高能量粒子。物理學者曾經測量到能量高達3.0 × 10²⁰ eV的粒子^[99]。當這些粒子進入地球的大氣層，與大氣層的核子發生碰撞時，會生成一射叢的粒子，包括π介子^[100]。緲子是一種輕子，是由π介子在高層大氣衰變而產生的。在地球表面觀測到的宇宙線，超過半數是緲子。半衰期為2.2微秒的緲子會因衰變而產生一個電子或正子。正確的π⁻介子反應式為^[101]

π−⇒μ−+ν¯μ{displaystyle mathrm {pi } ^{-}Rightarrow mathrm {mu } ^{-}+{bar {mathrm {nu } }}_{mathrm {mu } },!}，

μ−⇒e−+ν¯e+νμ{displaystyle mathrm {mu } ^{-}Rightarrow mathrm {e} ^{-}+{bar {mathrm {nu } }}_{mathrm {e} }+mathrm {nu } _{mathrm {mu } },!}；

其中，μ−{displaystyle mathrm {mu } ^{-},!} 是緲子，νμ{displaystyle mathrm {nu } _{mathrm {mu } },!} 是緲微中子，ν¯μ{displaystyle {bar {mathrm {nu } }}_{mathrm {mu } },!} 是反緲微中子，ν¯e{displaystyle {bar {mathrm {nu } }}_{mathrm {e} },!} 是反電微中子。

觀測

電漿燈內部的電子與離子重結合以後，從激發態躍遷至較低能級的量子態，同時釋放出電磁輻射。由於電磁輻射的頻率與電漿材料的性質有關，因而會顯示出各種不同的顏色。

靠著偵測電子的輻射能量，天文學家可以遠距離地觀測到電子的各種現象。例如，在像恆星日冕一類的高能量環境裏，自由電子會形成一種藉著制動輻射來輻射能量的電漿。電子氣體的電漿振盪是一種波動，是由電子密度的快速震盪所產生的波動。這種波動會造成能量的發射。天文學家可以使用無線電望遠鏡來偵測這能量^[102]。

根據普朗克關係式，光子的頻率與能量成正比。當一個束縛電子躍遷於原子的不同能級的軌域之間時，束縛電子會吸收或發射具有特定頻率的光子。例如，當照射寬帶光譜的光源所產生的光波於原子時，特徵吸收光譜會出現於透射輻射的光譜。每一種元素或分子會顯示出一組特徵吸收光譜，像氫光譜。光譜學專門研究光譜線的強度和寬度。細心分析這些數據，即可得知物質的組成元素和物理性質^[103]。

在實驗室操控條件下，電子與其它粒子的交互作用，可以用粒子偵測器來仔細觀察。電子的特徵性質，像質量、自旋和電荷等等，都可以加以測量檢驗。四極離子阱和潘寧阱可以長時間地將帶電粒子限制於一個很小的區域。這樣，科學家可以準確地測量帶電粒子的性質。例如，在一次實驗中，一個電子被限制於潘寧阱的時間長達10個月之久^[104]。1980年，由於各種先端科技的成功發展，電子磁矩的實驗值已經達到11個位數的精確度。在那時候，是所有由實驗得到的物理常數中，精確度最高的物理常數^[105]。

2008年2月，隆德大學的一組物理團隊首先拍攝到電子能量分佈的視訊影像。科學家使用非常短暫的閃光，稱為阿托秒脈衝，率先捕捉到電子的實際運動狀況^[106]。

在固態物質內，電子的分佈可以用角分辨光電子能譜學來顯像。應用光電效應理論，這科技照射高能量輻射於樣品，然後測量光電發射的電子動能分佈和方向分佈等等數據。仔細地分析這些數據，即可推論固態物質的電子結構^[107]。

應用領域

電子束

在一次美國太空總署的風洞試驗中，電子束射向太空梭的迷你模型，模擬返回大氣層時，太空梭四週的游離氣體^[108]。

電子束焊接（英语：electron beam welding）是應用於焊接領域的電子束科技。這焊接技術能夠將高達10⁷瓦特／公分²能量密度的熱能，聚焦於直徑為0.3–1.3公釐的微小區域。使用這技術，技工可以焊接更深厚的物件，限制大部分熱能於狹窄的區域，而不會改變附近物質的材質。為了避免物質被氧化的可能性，電子束焊接必須在真空內進行。不適合使用普通方法焊接的傳導性物質，可以考慮使用電子束焊接。在核子工程和航天工程裏，有些高價值焊接工件不能接受任何瑕疵。這時候，工程師時常會選擇使用電子束焊接來達成任務^[109][110]。

電子束平版印刷術是一種分辨率小於1公釐的蝕刻半導體的方法。這種技術的缺點是成本高昂、程序緩慢、必須操作於真空內、還有，電子束在固體內很快就會散開，很難維持聚焦。最後這缺點限制住分辨率不能小於10奈米。因此，電子束平版印刷術主要是用來製造少數量特別的積體電路^[111]。

電子束照射（英语：electron irradiation）技術使用電子束來照射物質。爲了要改變物質的物理性質或滅除醫療物品和食品所含有的微生物，可以考慮使用電子束照射技術^[112]。做為放射線療法的一種，直線型加速器（英语：loinear particle accelerator）製備的電子束可以用來照射淺表性腫瘤。由於在被吸收之前，電子束只會穿透有限的深度（能量為5–20 MeV的電子束通常可以穿透5公分的生物體），電子束療法（英语：electron therapy）可以用來醫療像基底細胞癌（英语：basal cell carcinoma）一類的皮膚病。電子束療法也可以輔助治療已被X-射線照射過的區域^[113]。

粒子加速器使用電場來增加電子或正子的能量，使這些粒子擁有高能量。當這些粒子通過磁場時，它們會放射同步輻射。由於輻射的強度與自旋有關，因而造成了電子束的偏振。這過程稱為索克洛夫-特諾夫效應（英语：Sokolov–Ternov effect）。很多實驗都需要使用偏振的電子束為粒子源。同步輻射也可以用來降低電子束溫度，減少粒子的動量偏差。一當粒子達到要求的能量，使電子束和正子束發生互相碰撞與湮滅，這會引起能量的發射。偵測這些能量的分佈，仔細研究分析實驗數據，物理學家可以了解電子與正子碰撞與湮滅的物理行為^[114]。

成像

低能電子繞射技術（LEED）照射準直電子束（collimated electron beam）於晶體物質，然後根據觀測到的繞射圖樣，來推斷物質結構。這技術所使用的電子能量通常在20–200 eV之間^[115]。反射高能電子繞射（英语：reflection high energy electron diffraction）（RHEED）技術以低角度照射準直電子束於晶體物質，然後蒐集反射圖樣的數據，從而推斷晶體表面的資料。這技術所使用的電子的能量在8–20 keV之間，入射角度為1–4°^[116]。

電子顯微鏡將聚焦的電子束入射於樣本。由於電子束與樣本的交互作用，電子的性質，像移動方向、相對相位和能量，都會有所改變。細心地分析這些實驗蒐集到的數據，即可得到分辨率為原子尺寸的影像^[117]。使用藍色光，普通的光學顯微鏡的分辨率，因受到繞射限制，只能達到200奈米；相互比較，電子顯微鏡的分辨率，則是受到電子的德布羅意波長限制，對於能量為100 keV的電子，分辨率大約為0.0037奈米^[118]。像差修正穿透式電子顯微鏡（英语：Transmission Electron Aberration-corrected Microscope）能夠將分辨率降到低於0.05奈米，能夠清楚地觀測到個別原子^[119]。這能力使得電子顯微鏡成為，在實驗室裏，高分辨率成像不可缺少的儀器。但是，電子顯微鏡的價錢昂貴，保養不易。在操作電子顯微鏡時，樣品環境需要維持真空，科學家無法觀測活生物^[120]。

電子顯微鏡主要分為兩種類式：穿透式和掃描式。穿透式電子顯微鏡的操作原理類似高架式投影機，將電子束對準於樣品切片發射，穿透過的電子再用透鏡投影於底片或電荷耦合元件。掃描電子顯微鏡用聚焦的電子束掃瞄過樣品，就好像在顯示機內的光柵掃瞄。這兩種電子顯微鏡的放大率可從100倍到1,000,000倍，甚至更高。應用量子穿隧效應，掃描隧道顯微鏡將電子從尖銳的金屬針尖穿隧至樣品表面。為了要維持穩定的電流，針尖會隨著樣品表面的高低而移動，這樣，即可得到分辨率為原子尺寸的樣本表面影像^[121]。

自由電子雷射

在自由電子雷射裡，相對論性電子束會移動通過一對波盪器（英语：undulator）。每一個波盪器是由一排磁偶極矩組成，其磁場的磁偶極矩交替地指向相反方向。由於這些磁場的作用，電子會發射同步輻射；而這輻射會相干地與電子交互作用，會在共振頻率引起輻射場的強烈放大。自由電子雷射能夠發射相干的高輻射率的電磁輻射，而且頻域相當寬廣，從微波到軟X-射線。這元件可以應用於製造業、通訊業和各種醫療用途，像軟組織手術。^[122]

現階段已運行的自由電子雷射有美國史丹福直線加速器中心的直線加速器相干光源（LCLS）、^[123]德國電子加速器的漢堡自由電子雷射（Free-electron LASer in Hamburg, FLASH）^[124]與正在建造的歐洲X射線自由電子雷射（英语：European x-ray free electron laser）（E-XFEL）。建成之後，E-XFEL將會是世界上規模最大，能量最高的自由電子雷射裝置^[125][126]。

其它

陰極射線管的核心概念為，勞侖茲力定律的應用於電子束。陰極射線管廣泛的使用於實驗式儀器顯示器，電腦顯示器和電視。在光電倍增管內，每一個擊中光陰極（英语：photocathode）的光子會因為光電效應引起一堆電子被發射出來，造成可偵測的電流脈波^[127]。曾經在電子科技研發扮演重要的角色，真空管藉著電子的流動來操縱電子信號；但是，這元件現在已被電晶體一類的固態電子元件取代了。^[128]

參閱

註釋

1. 
   ^ 電子的帶電量是負基本電荷；質子的帶電量是正基本電荷。
   


2. 
   ^ 自旋的角動量 S{displaystyle S,!} 是從自旋量子數 s=1/2{displaystyle s=1/2,!} 計算而得：
   

   
   S=s(s+1)ℏ=32ℏ{displaystyle S={sqrt {s(s+1)}}hbar ={frac {sqrt {3}}{2}}hbar ,!}。

   
   


3. 
   ^
   從靜電學理論，一個半徑為 r{displaystyle r,!}，電荷量為 e{displaystyle e,!} 的圓球的勢能 Ep{displaystyle E_{mathrm {p} },!} 為
   

   
   Ep=12∫SσVda=e28πϵ0r{displaystyle E_{mathrm {p} }={frac {1}{2}}int _{mathcal {S}}sigma Vda={frac {e^{2}}{8pi epsilon _{0}r}},!}；

   
   其中，S{displaystyle {mathcal {S}},!} 是圓球表面，σ=e4πr2{displaystyle sigma ={frac {e}{4pi r^{2}}},!} 是面電荷密度，V=e4πϵ0r{displaystyle V={frac {e}{4pi epsilon _{0}r}},!} 是電勢，da{displaystyle da,!} 是微小面元素，ϵ0{displaystyle epsilon _{0},!} 是真空電容率。
   靜止質量為 m0{displaystyle m_{0},!} 的電子的靜止能量 E0{displaystyle E_{0},!} 是
   

   
   E0=m0c2{displaystyle E_{0}=m_{0}c^{2},!}；

   
   其中，c{displaystyle c,!} 是光速。
   設定這兩個公式等值，則可得到古典電子半徑 r{displaystyle r,!}。
   


4. 
   ^ ^4.04.1 雖然每一點表示一個電子抵達探測屏，這事實並不能表現出電子的粒子性，因為探測器是由離散原子組成的，這可以詮釋為電子波與離散原子彼此之間的局域相互作用，這是探測器的特性，但是探測這動作造成電子波的塌縮。^{[54]:sec iv}
   


5. 
   ^ 從波動觀分析，薛丁格方程式乃是一個波動方程式，它完美地描述一個與時間、位置有關的概率波所發生的運動行為與所具有的量子性質，而解答這波動方程式的波函數可以詮釋為「在某時間、某位置發生相互作用的概率幅」。這寬鬆的詮釋方式可以適用於波動觀或粒子觀。^[54]
   


6. 
   ^ 反對稱性波函數為 [sin⁡(x)sin(3y)−sin(3x)sin(y)]/2,  (0≤x,y≤π){displaystyle [sin(x)sin(3y)-sin(3x)sin(y)]/{sqrt {2}}, (0leq x,yleq pi )}。注意到在 x=y{displaystyle x=y} 附近，機率輻絕對值很微小，兩個費米子趨向於彼此互相遠離對方。
   


7. 
   ^ 根據海森堡不確定原理和質能方程式：
   

   
   Δt≤ℏ/ΔE=ℏ/mec2≈1.3×10−21 [sec]{displaystyle Delta tleq hbar /Delta E=hbar /m_{e}c^{2}approx 1.3times 10^{-21} [{text{sec}}],!}；

   
   
   其中，me{displaystyle m_{e},!} 是電子的質量。
   


8. 
   ^ 波長的差值 Δλ{displaystyle Delta lambda }，跟反衝的角度 θ{displaystyle theta } 有關。其關係為：
   

   
   Δλ=hmec(1−cos⁡θ){displaystyle Delta lambda ={frac {h}{m_{e}c}}(1-cos theta )}。

   
   


9. 
   ^ 計算電子的速度，答案為：
   

   
   v=c1 −γ−2≈c(1−0.5γ−2)=0.99999999995c{displaystyle v=c{sqrt {1 -gamma ^{-2}}}approx cleft(1-0.5gamma ^{-2}right)=0.999,999,999,95,c,!}。

   
   

參考文獻

查 论 编 粒子物理学 基本粒子 費米子 夸克 u u d d c c s s t t b b 輕子 e- e+ μ- μ+ τ- τ+ νe ve νμ vμ ντ vτ 玻色子 标量玻色子 H γ g W± Z0 复合粒子 強子 重子 · 核子 · 超子 p p n n Δ Λ Σ Ξ Ω 介子 · 夸克偶素 π K ρ D J/ψ Υ B 其它 原子核 原子 超原子 奇異原子 電子偶素 緲子偶素 真緲子偶素 介子偶素（英语：Onium） 介子原子 超子原子 反氢 介子核 超核 重味超核 分子 离子 假想的基本粒子 超對稱粒子 超規範子 超膠子 重力微子 其他 超軸子 超荷子 超胀子 超中性子 超希格斯粒子（英语：Higgsino） 超費米子 其它 大质量弱相互作用粒子（WIMP） 惰性中微子 胀子 马约拉纳费米子 m 加速子 快子 A0 G X Y W'（英语：W′_and_Z′_bosons） Z'（英语：W′_and_Z′_bosons） 鬼 假想的复合粒子 奇異強子 奇異重子 五夸克態 双重子态 奇異介子（英语：Exotic mesons） 膠球 混杂态 四夸克態 其它 介子分子（英语：Mesonic molecule） 準粒子 達維多夫孤子（英语：Davydov soliton） 量子滴（英语：Dropleton） 激子 空穴 磁振子 聲子 磁單極子 電漿子 電磁極化子 極子（英语：Polaron） 旋子 (準粒子)（英语：Roton） 列表 粒子列表 奇异原子列表 准粒子列表 重子列表 粒子发现年表 物理学主题