磁化強度
- 在這篇文章內,向量與标量分別用粗體與斜體顯示。例如,位置向量通常用 r{displaystyle mathbf {r} ,!}
表示;而其大小則用 r{displaystyle r,!}
來表示。
磁化強度(英语:magnetization),又稱磁化向量,是衡量物體的磁性的一個物理量,定義為單位體積的磁偶極矩,如下方程式:
M =def nm{displaystyle mathbf {M} {stackrel {def}{=}} nmathbf {m} };
其中,M{displaystyle mathbf {M} }


當施加外磁場於物質時,物質的內部會被磁化,會出現很多微小的磁偶極子。磁化強度描述物質被磁化的程度。採用國際單位制,磁化強度的單位是安培/公尺。
物質被磁化所產生的磁偶極矩有兩種起源。一種是由在原子內部的電子,由於外磁場的作用,其軌域運動產生的磁矩會做拉莫爾進動,從而產生的額外磁矩,累積凝聚而成。另外一種是在外加靜磁場後,物質內的粒子自旋發生「磁化」,趨於依照磁場方向排列。這些自旋構成的磁偶極子可視為一個個小磁鐵,可以以向量表示,作為自旋相關磁性分析的古典描述。例如,用於核磁共振現象中自旋動態的分析。
物質對於外磁場的響應,和物質本身任何已存在的磁偶極矩(例如,在鐵磁性物質內部的磁偶極矩),綜合起來,就是淨磁化強度。
在一個磁性物質的內部,磁化強度不一定是均勻的,磁化強度時常是位置向量的函數。
目录
1 馬克士威方程組
1.1 磁感應強度、磁場強度和磁化強度之間的關係
1.2 磁化電流
1.3 靜磁學
2 磁化動力學
3 磁性物質
3.1 抗磁性
3.2 順磁性
3.3 鐵磁性
3.4 反鐵磁性
3.5 亞鐵磁性
3.6 超順磁性
4 參閱
5 註釋
6 參考文獻
馬克士威方程組
馬克士威方程組描述磁感應強度 B{displaystyle mathbf {B} }






磁感應強度、磁場強度和磁化強度之間的關係
磁場強度 H{displaystyle mathbf {H} }
H =def 1μ0B−M{displaystyle mathbf {H} {stackrel {def}{=}} {frac {1}{mu _{0}}}mathbf {B} -mathbf {M} };
其中,μ0{displaystyle mu _{0}}
對於抗磁性物質和順磁性物質,M{displaystyle mathbf {M} }

M=χmH{displaystyle mathbf {M} =chi _{m}mathbf {H} };
其中,χm{displaystyle chi _{m}}
由於遲滯現象,鐵磁性物質的 M{displaystyle mathbf {M} }

磁化電流
在磁性物質內,「磁化電流」是總電流的一部分,又稱為「束縛電流」,是由束縛電荷形成的。磁性物質內部的「束縛電流密度」 Jb{displaystyle mathbf {J} _{b}}

Jb =def ∇×M{displaystyle mathbf {J} _{b} {stackrel {def}{=}} nabla times mathbf {M} }、
Kb =def M×n^{displaystyle mathbf {K} _{b} {stackrel {def}{=}} mathbf {M} times {hat {n}}};
其中,n^{displaystyle {hat {mathbf {n} }}}
在馬克士威方程組內的總電流 J{displaystyle mathbf {J} }
J=Jf+Jb+JP{displaystyle mathbf {J} =mathbf {J} _{f}+mathbf {J} _{b}+mathbf {J} _{P}};
其中,Jf{displaystyle mathbf {J} _{f}}

自由電流密度是由自由電荷形成的自由電流的密度。自由電荷不束縛於物質的原子的內部。
電極化電流是由含時電極化強度P{displaystyle mathbf {P} }
JP=∂P∂t{displaystyle mathbf {J} _{P}={frac {partial mathbf {P} }{partial t}}}。
靜磁學
除去自由電流和各種含時效應,描述磁現象的馬克士威方程組約化為
∇⋅H=−∇⋅M{displaystyle mathbf {nabla cdot H} =-nabla cdot mathbf {M} }、
∇×H=0{displaystyle mathbf {nabla times H} =0}。
應用類比方法,與靜電學問題類比:
∇⋅E=ρϵ0{displaystyle mathbf {nabla cdot E} ={frac {rho }{epsilon _{0}}}}、
∇×E=0{displaystyle mathbf {nabla times E} =0},
靜磁學的問題可以用靜電學的方法來解析。在這裏,∇⋅M{displaystyle nabla cdot mathbf {M} }

磁化動力學
當思考奈米尺寸和奈米時段的磁化作用時,含時磁化物理行為變得很重要。不單只是依著外磁場的磁場線排列,在物質內的單獨的磁偶極矩會開始繞著外磁場進動,通過弛豫,緩慢地隨著能量傳輸進入物質結構,達成與磁場線排列。
磁性物質

各種不同磁性的級列。[1]
抗磁性
抗磁性是物質抗拒外磁場的趨向,因此,會被磁場排斥。所有物質都具有抗磁性。可是,對於具有順磁性的物質,順磁性通常比較顯著,遮掩了抗磁性。[2] 只有純抗磁性物質才能明顯地被觀測到抗磁性。例如,惰性氣體元素和抗腐蝕金屬元素(金、銀、銅等等)都具有顯著的抗磁性。[3]
當外磁場存在時,抗磁性才會表現出來。假設外磁場被撤除,則抗磁性也會遁隱形跡。
在具有抗磁性的物質裏,所有電子都已成對,內秉電子磁矩不能集成宏觀效應。抗磁性的機制是電子軌域運動,用經典物理理論解釋如下:[4]
- 由於外磁場的作用,環繞著原子核的電子,其軌域運動產生的磁矩會做拉莫爾進動,從而產生額外電流與伴隨的額外磁矩。這額外磁矩與外磁場呈相反方向,抗拒外磁場的作用。由這機制所帶來的磁化率與溫度無關,以方程式表達為
χ=− μ0NZe26m⟨r2⟩{displaystyle chi =- {frac {mu _{0}NZe^{2}}{6m}}langle r^{2}rangle };
- 其中,μ0{displaystyle mu _{0}}
是磁常數,Z{displaystyle Z}
是原子數量密度,Z{displaystyle Z}
是原子序,m{displaystyle m}
是電子質量,r{displaystyle r}
是軌道半徑。⟨r2⟩{displaystyle langle r^{2}rangle }
是 r2{displaystyle r^{2}}
的量子力學平均值。
特別注意,這解釋只能用來啟發思考。正確的解釋需要依賴量子力學。
順磁性

對於順磁性物質、鐵磁性物質、反鐵磁性物質,磁化率與溫度之間的理論關係。[4]
鹼金屬元素和除了鐵、鈷、鎳以外的過渡元素都具有順磁性。[3]在順磁性物質內部,由於原子軌域或分子軌域只含有奇數個電子,會存在有很多未配對電子。遵守包立不相容原理,任何配對電子的自旋,其磁矩的方向都必需彼此相反。未配對電子可以自由地將磁矩指向任意方向。當施加外磁場時,這些未配對電子的磁矩趨於與外磁場呈相同方向,從而使磁場更加強烈。假設外磁場被撤除,則順磁性也會消失無蹤。
一般而言,除了金屬物質以外,[3]順磁性與溫度相關。由於熱騷動(thermal agitation)造成的碰撞會影響磁矩整齊排列,溫度越高,順磁性越微弱;溫度越低,順磁性越強烈。
在低磁場,足夠高溫的狀況,[註 1]根據居里定律(Curie's law),磁化率 χ{displaystyle chi }

χ=C/T{displaystyle chi =C/T};
其中,C{displaystyle C}
鐵磁性

磁化強度(豎軸)與H場(橫軸)之間的磁滯迴路關係。
在鐵磁性物質內部,如同順磁性物質,有很多未配對電子。由於交換作用(exchange interaction),這些電子的自旋趨於與相鄰未配對電子的自旋呈相同方向。由於鐵磁性物質內部又分為很多磁疇,雖然磁疇內部所有電子的自旋會單向排列,造成「飽合磁矩」,磁疇與磁疇之間,磁矩的方向與大小都不相同。所以,未被磁化的鐵磁性物質,其淨磁矩與磁化向量都等於零。
假設施加外磁場,這些磁疇的磁矩還趨於與外磁場呈相同方向,從而形成有可能相當強烈的磁化向量與其感應磁場。 隨著外磁場的增高,磁化強度也會增高,直到「飽和點」,淨磁矩等於飽合磁矩。這時,再增高外磁場也不會改變磁化強度。假設,現在減弱外磁場,磁化強度也會跟著減弱。但是不會與先前對於同一外磁場的磁化強度相同。磁化強度與外磁場的關係不是一一對應關係。磁化強度比外磁場的曲線形成了磁滯迴線。
假設再到達飽和點後,撤除外磁場,則鐵磁性物質仍能保存一些磁化的狀態,淨磁矩與磁化向量不等於零。所以,經過磁化處理後的鐵磁性物質具有「自發磁矩」。
每一種鐵磁性物質都具有自己獨特的居里溫度。假若溫度高過居里溫度,則鐵磁性物質會失去自發磁矩,從有序的「鐵磁相」轉變為無序的「順磁相」。這是因為熱力學的無序趨向,大大地超過了鐵磁性物質降低能量的有序趨向。根據居里-外斯定律(Curie-Weiss law),磁化率 χ{displaystyle chi }

χ=C/(T−Tc){displaystyle chi =C/(T-T_{c})};
其中,Tc{displaystyle T_{c}}
假設溫度低於居里溫度,則根據實驗得到的經驗公式,
ΔM(T)/M0=βT3/2{displaystyle Delta M(T)/M_{0}=beta T^{3/2}};
其中,ΔM(T)=M(T)−M0{displaystyle Delta M(T)=M(T)-M_{0}}





這與布洛赫溫度1.5次方定律(Bloch T3/2 law)的理論結果一致。
鎳、鐵、鈷、釓與它們的合金、化合物等等,這些常見的鐵磁性物質很容易做實驗顯示出其鐵磁性。
反鐵磁性
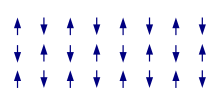
反鐵磁性的有序排列
在反鐵磁性物質內部,相鄰價電子的自旋趨於相反方向。這種物質的淨磁矩為零,不會產生磁場。這種物質比較不常見,大多數反鐵磁性物質只存在於低溫狀況。假設溫度超過奈爾溫度,則通常會變為具有順磁性。例如,鉻、錳、輕鑭系元素等等,都具有反鐵磁性。
當溫度高於奈爾溫度 TN{displaystyle T_{N}}


χ=2CT+TN{displaystyle chi ={frac {2C}{T+T_{N}}}}。
做實驗得到的經驗關係式為
χ=2CT+θ{displaystyle chi ={frac {2C}{T+theta }}};
其中,θ{displaystyle theta }

理論而言,當溫度低於奈爾溫度 TN{displaystyle T_{N}}
- 假設外磁場垂直於自旋,則垂直磁化率近似為常數 χ⊥≈C/TN{displaystyle chi _{perp }approx C/T_{N}}
。
- 假設外磁場平行於自旋,則在絕對溫度0K時,平行磁化率為零;在從0K到奈爾溫度 TN{displaystyle T_{N}}
之間,平行磁化率會從 χ∥(0)=0{displaystyle chi _{parallel }(0)=0}
平滑地單調遞增至 χ∥(TN)=C/TN{displaystyle chi _{parallel }(T_{N})=C/T_{N}}
。
亞鐵磁性
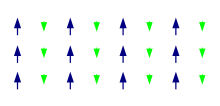
亞鐵磁性的有序排列
像鐵磁性物質一樣,當磁場不存在時,亞鐵磁性物質仍舊會保持磁化不變;又像反鐵磁性物質一樣,相鄰的電子自旋指向相反方向。這兩種性質並不互相矛盾,在亞鐵磁性物質內部,分別屬於不同次晶格的不同原子,其磁矩的方向相反,數值大小不相等,所以,物質的淨磁矩不等於0,磁化強度不等於零,具有較微弱的鐵磁性。
由於亞鐵磁性物質是絕緣體。處於高頻率時變磁場的亞鐵磁性物質,由於感應出的渦電流很少,可以允許微波穿過,所以可以做為像隔離器(isolator)、循環器(circulator)、回旋器(gyrator)等等微波器件的材料。
由於組成亞鐵磁性物質的成分必需分別具有至少兩種不同的磁矩,只有化合物或合金才會表現出亞鐵磁性。常見的亞鐵磁性物質有磁鐵礦(Fe3O4)、鐵氧體(ferrite)等等
超順磁性
當鐵磁體或亞鐵磁體的尺寸足夠小的時候,由於熱騷動影響,這些奈米粒子會隨機地改變方向。假設沒有外磁場,則通常它們不會表現出磁性。但是,假設施加外磁場,則它們會被磁化,就像順磁性一樣,而且磁化率超大於順磁體的磁化率。
參閱
- 磁導率
- 地球磁場
- 地磁逆轉
- 核磁共振
| ||||||||||||||||||||||||||||
註釋
^ 更確切地說,當 μB/KBT≫1{displaystyle mu B/K_{B}Tgg 1}時,居里定律成立;其中,μ{displaystyle mu }
是磁矩,KB{displaystyle K_{B}}
是波茲曼常數。
參考文獻
^ HP Meyers. Introductory solid state physics 2. CRC Press. 1997: 362; Figure 11.1. ISBN 0748406603.
^ Catherine Westbrook, Carolyn Kaut, Carolyn Kaut-Roth. MRI (Magnetic Resonance Imaging) in practice 2. Wiley-Blackwell. 1998: 217. ISBN 0632042052.
^ 3.03.13.2 Chen, Chih-Wen, Magnetism and metallurgy of soft magnetic materials, Courier Dover Publications: pp. 1, 7–8, 12, 1977, ISBN 9780486649979 引文格式1维护:冗余文本 (link)
^ 4.04.14.24.34.4 Kittel, Charles. Introduction to Solid State Physics 6th. John Wiley & Sons. 1986: pp. 299–302, 323–324, 330–335, 340–344, 351–352. ISBN 0-471-87474-4. 引文格式1维护:冗余文本 (link)
^ Chikazumi, Sōshin; Chad Graham. Physics of ferromagnetism 2nd. Oxford University Press. 2009: 140–142. ISBN 9780199564811. 引文使用过时参数coauthors (帮助)
