Cfxtrjtrk

本条目需要編修，以確保文法、用詞、语气、格式、標點等使用恰当。（2018年4月4日） 請按照校對指引，幫助编辑這個條目。（幫助、討論）

透過基隆河面反射的城市

胡德山在镜湖中的倒影

反射（英文：reflection），是一種物理現象，是指波阵面從一個介質進入另一個介質時，在两个介质的界面处，其傳播方向突然改變，而回到其來源的介質。常见的例子包括光、声波和水波的反射。反射定律指出，对于镜面反射，入射角等於反射角，即光線射入時的角度必與光線反射后的角度相等。镜面反射可以通过镜子观察到。

在声学方面，反射会引起回声，这在声纳上得到很好应用。在地质学方面，研究地震波时，反射是十分重要的部分。反射可以在水体的面波上被观察到，也可以在包括可见光在内的多种电磁波上被观察到。甚高频以及更高频的波的反射对于无线电传输和雷达十分重要。甚至硬X射线和伽马射线在角度较浅时，也可以被“擦边”镜反射。

光的反射

光的反射可以是镜面反射（如同镜子）或漫反射（保留了能量，但丢失了图像），取决于界面性质。

一面镜子就可以提供光的镜面反射的最常见模型，镜子往往由一块有着金属涂层的薄玻璃板组成，而这金属涂层才是反射实际发生的地方。反射在金属中会增强，因为金属对于超出它们集肤深度的波能起到抑制传播的作用。反射同样能在透明介质的界面上发生，例如水和玻璃。

镜面反射示意图

在示意图中，一束光线PO{displaystyle PO}在点O{displaystyle O}处射到了一面竖直镜子上，反射光线是OQ{displaystyle OQ}。在点O{displaystyle O}处作出一条假想的与镜面垂直的直线，叫做法线(normal)。有了法线，我们可以测量出入射角 θi{displaystyle theta _{i}}，和反射角 θr{displaystyle theta _{r}}。反射定律表述为θi=θr{displaystyle theta _{i}=theta _{r}}，换句话说，入射角等于反射角。

事实上，只要光从一个有着特定折射率的介质传播进入一个有着不同折射率的介质，光的反射就会发生。在绝大多数情况下，只有一部分光会从界面反射，余下的则会折射。通过解在一束光线射到一个界面上的情况下的麦克斯韦方程组，派生出了菲涅耳方程组，用它可以预测在特定情况下，多少光发生反射和多少光发生折射。这与阻抗失配在一个电回路中引起信号反射的方式类似。当光从光密介质入射时，如果入射角大于临界角，全内反射就会发生。

全内反射被用来使波集中，此时用一般方法不能将波有效地反射。X射线望远镜是通过为波创造一个辐辏“轨道”来建造的。波以低角度与这个轨道的表面相互作用，与此同时，它们也就朝着目标点反射（或是朝着与轨道表面的另一个相互作用点，最终被导向位于目的地的探测器）。普通的反光体此时无法发挥作用，因为X射线会轻易穿过设计好的反光体。

当光反射离开一个比外部介质更密（折射率更高）的材料时，它会经受一次极性倒转。反之，一个更疏、折射率更低的材料会使光同相位反射。这在薄膜光学领域中是一个重要法则。

镜面反射会形成图像。平坦表面上的反射形成的是镜像，它看起来是左右颠倒的，因为我们会把我们看到的图像，与我们在转到图像的位置后的所见作比较。在弯曲表面上的镜面反射会形成一个放大或缩小的图像；曲面镜拥有光学倍率。像这样的镜子可能会有着球形或是抛物面形的表面。

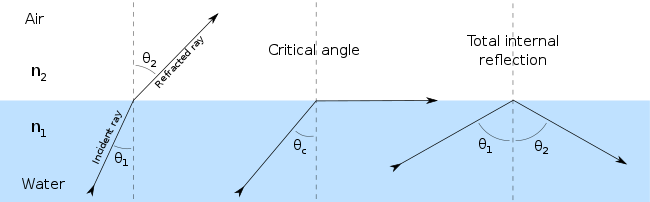
光在两种介质界面处发生的折射

反射定律

反射定律的一个例子

如果反射的表面非常光滑，光发生的反射就被称作镜面反射或单向反射。反射定律如下：

1. 入射光线、反射光线和反射面在反射发生处的法线位于同一个平面。


2. 入射光线与法线所成的角等于反射光线与同一条法线所成的角。


3. 反射光线和入射光线处在法线的相对两边。

这三条定律全部可以由菲涅尔方程组导出。

机制

播放媒体

二维模拟：量子粒子的反射。白色模糊部分表示测量时在特定区域发现一个粒子的概率分布。

在经典电动力学中，光被看作一种电磁波，一种通过麦克斯韦方程组描述的波。射到材料上的入射光导致了单个原子极化的微小振动（若是金属材料，则是电子的振动），造成了每一个粒子都向四面八方辐射出微弱的次级波，就像一个偶极子天线。根据惠更斯－菲涅耳原理，所有这些波加起来就给出了镜面反射和折射。

对于像玻璃这样的介电质，光的电场影响了材料里的电子，这些移动的电子形成了场并变成新的辐射体。玻璃中的折射光是向前的辐射与入射光的联合。反射光是所有电子产生的向后的辐射的联合。

在金属中，没有结合能的电子被称作自由电子。当这些电子随着入射光振动时，它们的辐射的场和入射光的场之间的相位差是π{displaystyle pi }(180°)，所以向前的辐射终止了入射光，而向后的辐射就是反射光。

在光量子方面的光-物质相互作用是量子电动力学的话题，详细的描述在理查德·费曼的畅销书QED：光和物质的奇妙理论中有所提及。

漫反射

固体表面发生漫反射的一般散射机制

当光射到一个（非金属的）材料表面上时，它会向各个方向弹离，这是因为材料内部极小的不规则（例如，多晶材料的晶粒边界，有机材料的细胞或纤维边界），或是因为材料的表面粗糙，因而发生了繁多的反射造成的。因此，不会形成“图像”。这被称作漫反射。反射的确切的样子取决于材料的结构。漫反射的一个普通的模型是朗伯反射率，此时光在各个方向以相同的亮度（光度学上）或辐射率（辐射度学上）进行反射，这在朗伯余弦定律中有描述。

大多数物体发送到我们眼中的光，都是由于它们表面发生了漫反射，所以这便是我们进行肉眼观察的主要机制。^[1]

逆反射

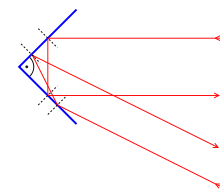
角反射器的工作原理

有些表面会展示出逆反射。这些表面的结构使之将光向射入的方向反射。

当飞过被太阳光照亮的云层时，飞行器的阴影周围的区域看起来更亮，相似的效果也会出现在草的露珠上。这种不完整的逆反射的产生，是因为水滴的弯曲表面具有折射的特性，而水滴的后边具有反射的特性。

一些动物的视网膜起到了逆反射器的作用，这有效地提高了动物的夜视能力。因为它们眼中的许多透镜往复地改变进出的光线的路径，眼睛就有了强的逆反射器一样的效果，所以当它们晚上在荒地上行走时，有时会看到它们的眼睛会发光。

将三面平常的镜子两两垂直地放置，就制成了一个简单的逆反射器（角反射器）。形成的图像与单面镜子所成的相反。在一个表面上放一层微小的具有折射能力的球，或创造一些金字塔形的结构，就可以让一个表面具有一部分的逆反射特性。在这两种情况下，内部的反射造成光向它发源的地方反射回去。这被用来使交通标志和汽车牌照能基本上将光反射回它射来的地方。在这种应用中，完美的逆反射并不是想要的，因为这样的话，光就会径直地向驶来的车的车灯射去，而不是射入司机的眼睛。

多重反射

当光从一面镜子反射出来，一个图像就会出现。两面精确面对面的镜子，就会显出一条直线上有无穷多个图像的样子。如果两面镜子成一定角度，在它们之间看到的多重图像就会位于一个圆上。^[2]那个圆的圆心位于镜子假想的相交处。四面镜子面对面排成方形，就会显出无穷多个图像排列在一个平面内的样子。如果每对镜子彼此都成一定角度，组成一个金字塔，那么在它们之间看到的多重图像就会位于一个球上。如果金字塔的底部是矩形，图像就会遍布一段环面。^[3]

注意这些都是在理想状况下的完美模型，需要把绝对光滑、绝对平坦、不吸收任何光的完美反射器完美地校准。实际中，这些情形只能去趋近却不能去达到，因为反射器表面的任何瑕疵造成的影响都会增加、放大，而对光的吸收会逐渐使图像黯淡、消失，而且所有的观测设备（生物的或技术的）都会有干扰。

复杂共轭反射

在这个过程中（也被理解为相位共轭），由于经过非线性的光学处理，光精确地向射来的方向反射回去。不仅光的方向颠倒了，而且实际的波阵面也被颠倒了。共轭反射器可以将光线反射，并使反射光再次通过有像差的光学仪器，因此可以用来消除像差。

其他类型的反射

中子反射

能反射中子的材料，例如铍，被用于核反应堆和核武器。在物理和生物科学中，将材料的原子中的中子反射出来普遍用于测定材料内部结构。

声反射

用于高频的声音扩散面板

当纵向的声波射到一个平坦表面上时，声音以一种连贯的方式反射，由反射面的大小与声音的波长相比有多大来提供。注意可听声的频率范围广泛（从20赫兹到大约17000赫兹），于是波长范围也很广泛（从大约20毫米到17米）。因此反射的总体特性会根据表面的质地和结构而变化。例如，多孔的材料会吸收一些能量，而粗糙（相对于波长而言）的材料往往向多方向反射——将能量扩散而不是协调一致地反射。这就引入了建筑声学的领域，因为这些反射的特性对于一个空间的听觉感受来说是挑剔的。在外部噪声控制的理论中，通过将一部分声音向相反方向反射，反射表面的大小会从隔音屏障的设想中得到轻微减损。

地震反射

由于地震或其他来源（例如爆炸）产生的地震波可能会被地球内部许多地层反射。研究地震引起的波的深度反射，使得地震学家可以测定地球的分层结构。更浅的反射通常被用于反射地震学来研究地球的地壳，尤其用于勘探石油和天然气储量。

參照

參考資料