偏振

橡膠細線的圓偏振運動,在經過一條狹縫之後,改變為線偏振運動。
偏振(polarization)指的是横波能夠朝著不同方向振盪的性質。例如電磁波、引力波都會展示出偏振現象。纵波则不會展示出偏振現象,例如傳播於氣體或液體的聲波,其只會朝著傳播方向振盪。如右圖所示,緊拉的細線可以展示出線偏振現象與圓偏振現象。
電磁波的電場與磁場彼此相互垂直。按照常規,電磁波的偏振方向指的是電場的偏振方向。在自由空間裏,電磁波是以橫波方式傳播,即電場與磁場又都垂直於電磁波的傳播方向。理論而言,只要垂直於傳播方向的方向,振盪的電場可以呈任意方向。假若電場的振盪只朝著單獨一個方向,則稱此為「線偏振」或「平面偏振」;假若電場的振盪方向是以電磁波的波頻率進行旋轉動作,並且電場向量的矢端隨著時間流意勾繪出圓型,則稱此為「圓偏振」;假若勾繪出橢圓型,則稱此為「橢圓偏振」;對於這兩個案例,又可按照在任意位置朝著源頭望去,電場隨時間流易而旋轉的順時針方向、逆時針方向,將圓偏振細分為「右旋圓偏振」、「左旋圓偏振」,將橢圓偏振細分為「右旋橢圓偏振」、「左旋橢圓偏振」;這性質稱為手徵性。
光波是一種電磁波。很多常見的光學物質都具有各向同性,例如玻璃。這些物質會維持波的偏振態不變,不會因偏振態的不同而展現出不同的物理行為。可是,有些重要的雙折射物質或光學活性物質具有各向異性。因此,偏振方向的不同,波的傳播狀況也不同,或者,波的偏振方向會被改變。起偏器是一種光學濾波器,只能讓朝著某特定方向偏振的光波通過,因此,可以將非偏振光變為偏振光。
在涉及到橫波傳播的科學領域,例如光學、地震學、無線電學、微波學等等,偏振是很重要的參數。激光、光纖通信、無線通信、雷達等等應用科技,都需要完善處理偏振問題。
極化的英文原文也是「polarization」,在英文文獻裏,偏振與極化兩個術語通用,都是使用同一個詞彙來表達,只有在中文文獻裏,才有不同的用法。一般來說,偏振指的是任何波動朝著某特定方向振盪的性質,而極化指的是各個帶電粒子因正負電荷在空間裡分離而產生的現象。
目录
1 歷史
2 理論概述
2.1 橫電磁波
2.2 偏振態
2.3 非偏振光
2.4 其它種類偏振
3 數學表述
3.1 偏振橢圓
3.2 瓊斯向量與瓊斯矩陣
3.3 斯托克斯參數與穆勒矩陣
4 偏振測量技術
4.1 測量應力
4.2 橢圓偏振測量術
4.3 地質學
4.4 地震學
4.5 化學
4.6 天文學
5 重要應用
5.1 偏光太陽鏡
5.2 天空中的偏振光
5.3 液晶顯示器
5.4 三維電影
5.5 動物視覺
5.6 圓偏振的角動量
6 參見
7 註釋
8 參考文獻
歷史

艾蒂安-路易·馬呂斯
丹麥科學家拉斯穆·巴多林(Rasmus Bartholin)於1669年發現了光束通過冰洲石(Iceland spar)時會出現雙折射現象,假設照射光束於冰洲石,則這光束會被折射為兩道光束,一道光束遵守普通的折射定律,稱為「尋常光」,另外一道光束不遵守普通的折射定律,稱為「非常光」。巴多林無法解釋這現象的物理機制。[1]:25後來,克里斯蒂安·惠更斯注意到這奇特現象,他在1690年著作《光論》的後半部裏,對這現象有很詳細的論述;他認為,由於空間可能存在有兩種不同物質,所以才會出現兩道光束,它們分別對應於兩個不同的波前以不同的速度傳播於空間,所以,這不是很不平常的現象,但是,惠更斯又發現,這兩道光束與原本光束的性質大不相同,將其中任何一道光束照射於第二塊冰洲石,則折射出來的兩道光束,其輻照度會因為繞著光束軸旋轉冰洲石而改變,有時候甚至只會剩成一道光束。惠更斯猜想光波是縱波,他想出的簡單波動理論不能對這現象給出解釋。艾薩克·牛頓猜測,雙折射現象意味著組成光束的粒子具有側面(垂直於移動方向)性質。[1]:25-28
1808年,法蘭西學術院提議,1810年物理獎比賽的題目為「對於雙折射給出數學理論,並且做實驗證實」。艾蒂安-路易·馬呂斯決定參與競爭。他做實驗觀察,日光照射於盧森堡宮的玻璃窗,然後被玻璃反射出來的光束,假若入射角度達到某特定數值,則這反射光與惠更斯觀察到的折射光具有類似的性質,他稱這性質為「偏振」性質。他猜想,組成光束的每一道光線都具有某種特別的不對稱性;當這些光線具有相同的不對稱性時,則光束具有偏振性;當這些光線的不對稱性分別機率地指向不同方向時,則光束具有非偏振性;當在這兩種案例之間時,則光束具有部分偏振性。不單是玻璃,任何透明的固體或液體都會產生這種現象。他又從實驗結果推論出馬呂斯定律,定量地給出偏振光通過檢偏器後的輻照度,考慮到偏振方向與檢偏器傳輸軸方向之間的夾角角度。這實驗極具創意,又得到了很豐碩的重要成果,馬呂思因此榮獲1810年的物理獎。馬呂思對於偏振現象做出諸多貢獻,後人尊稱他為「偏振之父」。[2]:2050-2051[3]:448
後來,奧古斯丁·菲涅耳與弗朗索瓦·阿拉戈合作研究偏振對於楊氏干涉實驗的影響,他們認為光波是縱波,呈縱向震盪,但是這縱波的概念無法合理解釋實驗結果。阿拉戈告訴托馬斯·楊這問題,托馬斯·楊大膽建議,假若光波是橫波,呈橫向震盪,則光波可以分解為兩個相互垂直的分量,或許這樣做可以對實驗結果給出解釋。果真,這建議清除了很多疑點。1817年,菲涅耳與阿拉戈將實驗結果定性總結為菲涅耳-阿拉戈定律(Fresnel-Arago laws),表述處於不同偏振態的光束彼此之間的干涉性質。之後,菲涅耳試圖進一步定量表述這實驗,他發展出的波動理論是一種振幅表述,主要是用光波的振幅與相位來作分析;振幅表述能夠定量地解釋偏振光的物理性質;但非偏振光或部分偏振光不具有穩定的振幅與相位,無法用振幅表述給予解釋。[4]:xiii-xv[3]:466
1852年,乔治·斯托克斯提出一種強度表述,能夠描述偏振光、非偏振光與部分偏振光的物理行為;只需要使用四個參數,後來稱為斯托克斯參數(Stokes parameters),就可以描述任何光束的偏振態,更重要地,這四個參數可以直接測量獲得。[4]:xiv-xv
那時,電磁學理論雜亂無章,詹姆斯·馬克士威將這些理論加以整合,於1865年提出馬克士威方程組。從這方程組,他推導出電磁波方程式,推論出光波是一種電磁波,可以用馬克士威方程組作精確描述。菲涅耳的波動理論是建立於一些貌似合理的假定,由於能夠正確描述光波的一些物理行為,例如,傳播、衍射、偏振等等,符合實驗得到的結果,所以才被學術界接受。從馬克士威方程組可以嚴格地推導出菲涅耳的波動理論,給予這理論堅實穩固的基礎。[4]:2
理論概述

從白熾燈(1)發射出的非偏振光(2)入射於傳輸軸為垂直方向的起偏器(3),透射出來的是垂直平面偏振光(4)。
大多數光源屬於非偏振光源,例如,太陽、白熾燈等等,因為它們所發射出的光波是由一組不同空間特徵、頻率(波長)、相位、偏振的光波隨機混合所組成。為了了解光波的偏振性質,最簡單的方法就是先只思考單色平面波,這種波是具有特定傳播方向、頻率、相位、振盪方向的正弦波。從研究平面波光學系統的性質與行為,可以對於一般案例給出預測,這是因為任何特定空間結構的光波都可以分解為一組不同頻率、不同振幅的平面波,稱為其角譜(angular spectrum)。[5]:55ff
橫電磁波
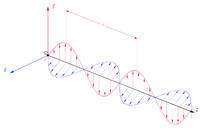
傳播於自由空間的電磁波是橫波,電場方向與磁場方向彼此相互垂直,又都垂直於傳播方向。
光波是一種電磁波。在自由空間裏,電磁波是橫波,其電場與磁場的方向都垂直於電磁波的傳播方向,並且相互垂直。[註 1]設想一個頻率為f{displaystyle f}


E(z,t)=E0ei(kz−2πft)=(x^E0x+y^E0y)ei(kz−2πft){displaystyle mathbf {E} (z,t)=mathbf {E} _{0}e^{i(kz-2pi ft)}=({hat {x}}E_{0x}+{hat {y}}E_{0y})e^{i(kz-2pi ft)}}、
B(z,t)=B0ei(kz−2πft)=(x^B0x+y^B0y)ei(kz−2πft){displaystyle mathbf {B} (z,t)=mathbf {B} _{0}e^{i(kz-2pi ft)}=({hat {x}}B_{0x}+{hat {y}}B_{0y})e^{i(kz-2pi ft)}};
其中,E0{displaystyle mathbf {E} _{0}}


E0{displaystyle mathbf {E} _{0}}





B0=μ0ϵ0z^×E0{displaystyle mathbf {B} _{0}={sqrt {mu _{0}epsilon _{0}}}{hat {z}}times mathbf {E} _{0}};
其中,ϵ0{displaystyle epsilon _{0}}

所以,從電磁波的電場可以計算出磁場。
類似地,在簡單介質裏,B0{displaystyle mathbf {B} _{0}}

B0=μϵz^×E0{displaystyle mathbf {B} _{0}={sqrt {mu epsilon }}{hat {z}}times mathbf {E} _{0}};
其中,ϵ{displaystyle epsilon }

所以,儘管電磁波傳播於簡單介質,仍舊可以從電磁波的電場計算出磁場。
由於E0{displaystyle mathbf {E} _{0}}




I=(|E0x|2+|E0y|2)/2η{displaystyle I=(|E_{0x}|^{2}+|E_{0y}|^{2})/2eta };
其中,η=μ/ϵ{displaystyle eta ={sqrt {mu /epsilon }}}
偏振與兩個分量的比率有關,在解析偏振問題時,可以約化為只思考|E0x|2+|E0y|2=1{displaystyle |E_{0x}|^{2}+|E_{0y}|^{2}=1}





E0x=1+Q2{displaystyle E_{0x}={sqrt {frac {1+Q}{2}}}}、
E0y=1−Q2eiϕ{displaystyle E_{0y}={sqrt {frac {1-Q}{2}}},e^{iphi }};
其中,Q{displaystyle Q}


按照常規,當提到偏振時,假若沒有特別設定,通常指的是電場的偏振。磁場的偏振通常與電場類似,唯一不同之處是90°空間角度差。
偏振態
@media all and (max-width:720px){.mw-parser-output .tmulti>.thumbinner{width:100%!important;max-width:none!important}.mw-parser-output .tmulti .tsingle{float:none!important;max-width:none!important;width:100%!important;text-align:center}}



在正弦波的每一個周期,電場向量和磁場向量都會描繪出一個橢圓形(注意到線偏振與圓偏振是橢圓偏振的特別案例)。這橢圓的形狀與定向定義了電磁波的偏振態。右圖展示出幾種不同種類的偏振。假設電場的x-分量、y-分量完全同相,則隨著時間流易,電場向量的矢端對於xy-平面的投射,會描繪出一條直線段,這案例因此稱為「線偏振」,又稱為「平面偏振」。假設電場的x-分量、y-分量擁有同樣的振輻,但是失相90°,則隨著時間流易,電場向量的矢端對於xy-平面的投射,會描繪出一條圓圈,這案例因此稱為「圓偏振」。根據光學領域常規,依相位差為-90°或+90°,圓偏振又分為右旋圓偏振(順時針旋轉)或左旋圓偏振(逆時針旋轉)。[6]:327-328假設除了失相以外,兩個分量的振輻不同,則隨著時間流易,電場向量的矢端對於xy-平面的投射,會描繪出一條橢圓,這案例因此稱為「橢圓偏振」。類似地,對應於不同的偏振態,電場的順時針旋轉或逆時針旋轉可以製成同樣的橢圓形狀。[8]:25-28
只要光波的傳播方向與z-軸同向,而xy-平面的定向可以任意選擇,就能夠正確地表現每一種偏振態。在解析問題時,通常會選擇合適的坐標軸,例如,光波的入射方向與x-軸同平面。另外,任意兩個相互正交的偏振態可以設定為基底函數;這樣,任意偏振態可以用基底函數來表示,例如,設定兩個相互正交的線偏振態為基底函數,則可很自然地處理表面反射、雙折射等問題。右旋圓偏振態與左旋圓偏振態也是很有用的選擇,可以用來研究光波傳播於立體異構的問題。[9]:49-50
非偏振光
可見光的大多數常見光源,包括黑體輻射、螢光等,會發射出不相干光波。在這些光源物質裏,處於激發態的原子或分子會獨立、毫無關聯地發射出這些隨機偏振的電磁輻射波列。每個波列持續大約10-8秒,所以,光波的偏振只能保持不變不超過10-8秒。這種光波稱為「非偏振光」。這術語所傳達出的意思並不精準,因為在任意時刻、任意位置,電場與磁場的方向都很明確,這術語所要傳達出的意思為,偏振隨時間流易而改變的速度非常快,它不是無法被測量到,就是與實驗結果無關。偏振光在通過消偏器(depolarizer)之後,由於透射光的偏振隨時間流易而改變的速率非常快,實際而言,可以忽略透射光在任意時刻的偏振,因此將透射光歸類為「非偏振光」。
假若光波的一個偏振模的功率與另一個偏振模的功率不一樣,則可稱此光波為「部分偏振光」。它可以統計描述為一個完全非偏振光與一個完全偏振光的疊加。[6]:330偏振度(degree of polarization)是光波的偏振部分所佔有的百分比,可以用來描述光波的成分。部分偏振態最常用斯托克斯參數(Stokes parameters)來設定。[6]:351,374-375
其它種類偏振

上图是角向偏振,下图是径向偏振。
除了橫波以外,很多種波動的振盪方向不局限為垂直於傳播方向。這些案例超過本條目範疇,本條目專注於橫波,可是,在有些案例裏,相干波的偏振不能簡單地用瓊斯向量或斯托克斯向量描述。
設想先前提到的傳播於均勻、各向同性、非衰減性介質的電磁平面波,假設改為傳播於各向異性介質,例如雙折射晶體,電場或磁場可能還會擁有縱場。對於這種案例,因為介質具有各向異性,它的電極化率或磁導率必需用張量來描述,電場的方向可能不同於電位移的方向,磁場強度的方向可能不同於磁場的方向。[10]:179-184[11]:51-52有些各向同性介質的折射率是複數,折射率的很大一部分是虛數,例如,金屬。甚至在這些介質裏,非均勻波都可以傳播;嚴格而說,它的各個場並不完全是橫場。表面波、傳播於波導或光纖的電磁波通常不是橫波,但是可以以橫模(transverse mode)的概念來描述。橫模又分為「橫電模」、「橫磁模」、「橫電磁模」、「混合模」四種。[10]:405-408
在自由空間裏,縱場分量可以被生成於平面波近似不成立的焦區。舉一個極端例子,在徑向偏振(radial polarization)光或角向偏振(azimuthal polarization)光的焦點,電場與磁場完全是縱場,與傳播方向同向。[12]

引力波的十字型偏振h+與交叉型偏振h×對於排列成圓圈形狀的粒子所產生的振盪效應。
像在流體裏傳播的聲波一類的縱波,振盪方向按照定義是沿著傳播方向,所以,偏振這論題通常不會被提出。從另一方面來說,在大塊固體傳播的聲波也可能是橫波,也可能是縱波,總共有三個偏振分量。對於這案例,橫偏振伴隨剪應力的方向,位移方向垂直於傳播方向;縱偏振描述固體的壓縮與振盪沿著傳播方向。在地震學裏,橫偏振與縱偏振之間的傳播差別是很重要的參數。[13]:56-57
傳遞引力的引力子不帶質量,具有橫向偏振,[14]:240-241因此引力波是橫波,引力波的振盪方向垂直於傳播方向,具有偏振性質。引力波可以呈兩種偏振態,十字型偏振h+與交叉型偏振h×。如右圖所示,假設一群粒子靜止排列成圓圈形狀,垂直於這圓圈傳播通過的引力波,其h+偏振會對這些粒子造成可觀察到的效應,在某一時刻,它會使得圓圈朝著上下方向拉伸,同時又會朝著左右方向壓縮;過一會兒,它又會將這變化逆轉回來。類似地,h×偏振會對這些粒子造成振盪效應。這兩種偏振態很相似,將其中一種偏振態旋轉45度,就可以得到另一種偏振態。[15]:210
數學表述
偏振橢圓

偏振橢圓圖。
「偏振橢圓」可以幫助想像與理解偏振問題。假設橫電磁波E(z,t){displaystyle mathbf {E} (z,t)}
Ex=E0xcos(kz−ωt+φx){displaystyle E_{x}=E_{0x}cos(kz-omega t+varphi _{x})}、
Ey=E0ycos(kz−ωt+φy){displaystyle E_{y}=E_{0y}cos(kz-omega t+varphi _{y})};
其中,E0x{displaystyle E_{0x}}



如右圖所示,這個橫電磁波的偏振橢圓以方程表示為[16]:7-9[4]:29-30[17]:6-8
(ExE0x)2+(EyE0y)2−2(ExE0x)(EyE0y)cosφ=sin2φ{displaystyle left({frac {E_{x}}{E_{0x}}}right)^{2}+left({frac {E_{y}}{E_{0y}}}right)^{2}-2left({frac {E_{x}}{E_{0x}}}right)left({frac {E_{y}}{E_{0y}}}right)cos varphi =sin ^{2}varphi };
其中,φ=φx−φy{displaystyle varphi =varphi _{x}-varphi _{y}}
「橢圓幅」A{displaystyle A}
A=E0x2+E0y2{displaystyle A={sqrt {E_{0x}^{2}+E_{0y}^{2}}}}。
「定向角」ψ{displaystyle psi }
tan(2ψ)=2E0xE0ycosφE0x2−E0y2,0≤ψ≤π{displaystyle tan(2psi )={frac {2E_{0x}E_{0y}cos varphi }{E_{0x}^{2}-E_{0y}^{2}}},qquad 0leq psi leq pi }。
「橢圓角」χ{displaystyle chi }
sin(2χ)=2E0xE0ysinφE0x2+E0y2,−π/4<χ≤π/4{displaystyle sin(2chi )={frac {2E_{0x}E_{0y}sin varphi }{E_{0x}^{2}+E_{0y}^{2}}},qquad -pi /4<chi leq pi /4}。
偏振橢圓是由橢圓幅、定向角、橢圓角設定。電磁波的偏振方向是由定向角、橢圓角設定。[17]:6-8
換另一種寫法,定義附屬角α{displaystyle alpha }
tanα=E0y/E0x,0≤α≤π/2{displaystyle tan alpha =E_{0y}/E_{0x},qquad 0leq alpha leq pi /2},
則定向角、橢圓角可以寫為
tan(2ψ)=tan(2α)cosφ{displaystyle tan(2psi )=tan(2alpha )cos varphi }、
sin(2χ)=sin(2α)sinφ{displaystyle sin(2chi )=sin(2alpha )sin varphi }。
設定ξ(t){displaystyle xi (t)}






tanξ(t)=Ey(z0,t)Ex(z0,t){displaystyle tanxi (t)={frac {E_{y}(z_{0},t)}{E_{x}(z_{0},t)}}}。
導數與相位差φ{displaystyle varphi }
∂ξ(t)∂t∝−sinφ{displaystyle {frac {partial xi (t)}{partial t}}propto -sin varphi }。
所以,假若相位差0<φ≤π{displaystyle 0<varphi leq pi }



在十九世紀,偏振橢圓是唯一能幫助想像與理解偏振問題的方法。但是,這方法有個缺點,假若光束必須傳播通過很多偏振器材,描述偏振行為的方程會變得很煩雜,很難找到解答。一直等到1892年,昂利·龐加萊提出龐加萊球(Poincaré sphere)後,才有了更好的解析方法。[18]:43
瓊斯向量與瓊斯矩陣
瓊斯向量可以用來描述完全偏振光;它不能用來描述非偏振光與部分偏振光。假設橫電磁波E(z,t){displaystyle mathbf {E} (z,t)}
Ex=E0xei(kz−ωt+φx){displaystyle E_{x}=E_{0x}e^{i(kz-omega t+varphi _{x})}}、
Ey=E0yei(kz−ωt+φy){displaystyle E_{y}=E_{0y}e^{i(kz-omega t+varphi _{y})}};
其中,E0x{displaystyle E_{0x}}



這橫電磁波的瓊斯向量J{displaystyle mathbf {J} }
J=(E0xeiφxE0yeiφy){displaystyle mathbf {J} ={binom {E_{0x}e^{ivarphi _{x}}}{E_{0y}e^{ivarphi _{y}}}}}。
通常,瓊斯向量會被歸一化成為單位向量。通過歸一化後,幾個常用的瓊斯向量可以很容易地被辨認出來。例如,平行於x-軸的線偏振(水平偏振)、平行於y-軸的線偏振(垂直偏振),它們的瓊斯向量Jh{displaystyle mathbf {J} _{h}}

Jh=(10)Jv=(01){displaystyle mathbf {J} _{h}={binom {1}{0}}qquad qquad mathbf {J} _{v}={binom {0}{1}}}。
左旋圓偏振、右旋圓偏振的瓊斯向量JL{displaystyle mathbf {J} _{L}}

JL=12(1−i)JR=12(1+i){displaystyle mathbf {J} _{L}={frac {1}{sqrt {2}}}{binom {1}{-i}}qquad qquad mathbf {J} _{R}={frac {1}{sqrt {2}}}{binom {1}{+i}}}。
兩個偏振態E1{displaystyle mathbf {E} _{1}}



J1⋅J2∗=0{displaystyle mathbf {J} _{1}cdot mathbf {J} _{2}^{*}=0}。
因此,水平偏振態與垂直偏振態相互正交,因為Jh{displaystyle mathbf {J} _{h}}

Jh⋅Jv∗=0{displaystyle mathbf {J} _{h}cdot mathbf {J} _{v}^{*}=0};
左旋圓偏振態與右旋圓偏振態相互正交,因為JL{displaystyle mathbf {J} _{L}}

JL⋅JR∗=0{displaystyle mathbf {J} _{L}cdot mathbf {J} _{R}^{*}=0}。
這些相互正交的瓊斯向量對形成一個基底,可以用來表示任意瓊斯向量。例如,JL{displaystyle mathbf {J} _{L}}

瓊斯矩陣是作用於瓊斯向量的算符。在實際實驗裏,瓊斯矩陣是由各種光學元件實現,例如,透鏡、分光器、鏡子等等。舉個簡單例子,水平線性偏振片、垂直線性偏振片的瓊斯矩陣分別為[6]:377-379
Mh=(1000)Mv=(0001){displaystyle mathbb {M} _{h}={begin{pmatrix}1&0\0&0end{pmatrix}}qquad qquad mathbb {M} _{v}={begin{pmatrix}0&0\0&1end{pmatrix}}}。
給定入射光為左旋圓偏振光JL{displaystyle mathbf {J} _{L}}

J=MhJL=(1000)12(1−i)=12(10){displaystyle mathbf {J} =mathbb {M} _{h}mathbf {J} _{L}={begin{pmatrix}1&0\0&0end{pmatrix}}{frac {1}{sqrt {2}}}{binom {1}{-i}}={frac {1}{sqrt {2}}}{binom {1}{0}}}。
斯托克斯參數與穆勒矩陣
非偏振光與部分偏振光不能用瓊斯向量來描述,必需使用斯托克斯參數才能正確描述。斯托克斯參數S0{displaystyle S_{0}}








S0=I0{displaystyle S_{0}=I_{0}}、
S1=I1−I0{displaystyle S_{1}=I_{1}-I_{0}}、
S2=I2−I0{displaystyle S_{2}=I_{2}-I_{0}}、
S3=I3−I0{displaystyle S_{3}=I_{3}-I_{0}}。
只要測量光束的I0{displaystyle I_{0}}




龐加萊球圖。Ip=I0P{displaystyle I_{p}=I_{0}{mathcal {P}}}
 。
。為了便利運算,將斯托克斯參數組成一個向量,稱為「斯托克斯向量」。[註 3]斯托克斯參數與輻照度、偏振度P{displaystyle {mathcal {P}}}
S0=I0{displaystyle S_{0}=I_{0}}、
S1=I0Pcos2ψcos2χ{displaystyle S_{1}=I_{0}{mathcal {P}}cos 2psi cos 2chi }、
S2=I0Psin2ψcos2χ{displaystyle S_{2}=I_{0}{mathcal {P}}sin 2psi cos 2chi }、
S3=I0Psin2χ{displaystyle S_{3}=I_{0}{mathcal {P}}sin 2chi }。
對於偏振光,P=1{displaystyle {mathcal {P}}=1}
S02=S12+S22+S32{displaystyle S_{0},^{2}=S_{1},^{2}+S_{2},^{2}+S_{3},^{2}}。
對於非偏振光,P=0{displaystyle {mathcal {P}}=0}

Sn=(S0000){displaystyle mathbf {S} _{n}={begin{pmatrix}S_{0}\0\0\0\end{pmatrix}}}。
部分偏振光是偏振光與非偏振光的權重組合:
S=(S0S1S2S3)=(1−P)(S0000)+P(S0S1′S2′S3′){displaystyle mathbf {S} ={begin{pmatrix}S_{0}\S_{1}\S_{2}\S_{3}\end{pmatrix}}=(1-{mathcal {P}}){begin{pmatrix}S_{0}\0\0\0\end{pmatrix}}+{mathcal {P}}{begin{pmatrix}S_{0}\S_{1}'\S_{2}'\S_{3}'\end{pmatrix}}}。
部分偏振光的偏振度P{displaystyle {mathcal {P}}}
P=S12+S22+S32/S0,0≤P≤1{displaystyle {mathcal {P}}={sqrt {S_{1},^{2}+S_{2},^{2}+S_{3},^{2}}}/S_{0},qquad 0leq {mathcal {P}}leq 1}。
通常,整個斯托克斯向量會被除以S0{displaystyle S_{0}}
Sh=(1100)Sv=(1−100){displaystyle mathbf {S} _{h}={begin{pmatrix}1\1\0\0\end{pmatrix}}qquad qquad mathbf {S} _{v}={begin{pmatrix}1\-1\0\0\end{pmatrix}}}。
光學元件作用於光束的效應必須用穆勒矩陣估算。一般而言,每一種實際光學元件都有其對應的穆勒矩陣,這是瓊斯矩陣的延伸至非偏振光與部分偏振光論題。穆勒矩陣是一個4×4實值矩陣。[16]:17例如,水平線性偏振片、垂直線性偏振片的瓊斯矩陣分別為[6]:377-379
Mh=12(1100110000000000)Mv=12(1−100−110000000000){displaystyle mathbb {M} _{h}={frac {1}{2}}{begin{pmatrix}1&1&0&0\1&1&0&0\0&0&0&0\0&0&0&0\end{pmatrix}}qquad qquad mathbb {M} _{v}={frac {1}{2}}{begin{pmatrix}1&-1&0&0\-1&1&0&0\0&0&0&0\0&0&0&0\end{pmatrix}}}。
給定入射光的斯托克斯向量S{displaystyle mathbf {S} }


S′=MS{displaystyle mathbf {S} '=mathbb {M} mathbf {S} }。
例如,假設入射光為非偏振光Sn{displaystyle mathbf {S} _{n}}

S=MhSn=12(1100110000000000)(1000)=12(1100){displaystyle mathbf {S} =mathbb {M} _{h}mathbf {S} _{n}={frac {1}{2}}{begin{pmatrix}1&1&0&0\1&1&0&0\0&0&0&0\0&0&0&0\end{pmatrix}}{begin{pmatrix}1\0\0\0\end{pmatrix}}={frac {1}{2}}{begin{pmatrix}1\1\0\0\end{pmatrix}}}。
更進階的矩陣方法涉及到相干矩陣(coherency matrix)的表述。[19]:137-142
偏振測量技術
測量應力

平面偏光仪工作示意图。

使用偏光儀,可以觀察到塑膠玻璃感受到的應力。
假若兩塊不同類型的偏振片分別製成的兩種偏振光相互正交,則稱它們為「正交偏振片」。例如,水平偏振片與垂直偏振片分別製成的水平偏振光與垂直偏振光相互正交,它們是兩塊正交偏振片。類似地,左旋圓偏振片與右旋圓偏振片也是兩塊正交偏振片。這實驗設置簡單地組成偏光儀(polariscope),又稱「偏振光鏡」;光束最先入射的偏振片為起偏器,然後再入射的偏振片為檢偏器;水平偏振片與垂直偏振片共同組成「平面偏光儀」;左旋圓偏振片與右旋圓偏振片共同組成「圓偏光儀」。如右圖所示,假設照射光束於由水平偏振片製成的起偏器,因為透射過的水平偏振光會被由垂直偏振片製成的檢偏器吸收,不能透射過垂直偏振片;所以,光束無法通過兩塊正交偏振片共同組成的偏光儀,透射的幅照度為零。但是假設將雙折射物質置入偏光儀內,即兩塊正交偏振片之間,光束在通過雙折射物質的過程中,偏振會被旋轉,因此可以從偏光儀觀察到透射光的色彩圖樣,並且測量到其幅照度。[2]:2142
各向同性固體不會顯示出雙折射現象。但是,假設施加機械應力,則會發生雙折射現象。製造塑膠成品的注射成型過程可能會將所施加的機械應力冷凍在塑膠成品裏。偏光儀可以用來分析雙折射物質所感受到的應力與應變。將雙折射物質置入偏光儀內,從測量到在任意位置的透射幅照度,可以估算在雙折射物質對應位置所感受到的應力與應變。光彈性法(photoelasticity)應用這偏振理論來分析固體所感受到的機械應力。這是一種極具功能的實驗方法,在結構工程學與機械工程學有廣泛的用途。[20]:167-170
橢圓偏振測量術
橢圓偏振測量術是一種用途極廣的技術,可用來測量均勻表面的光學性質;簡略描述其程序,就是在均勻表面做鏡面反射後,測量光波的偏振態的改變;通常這函數的參數為入射角與波長。由於橢圓偏振測量術倚賴反射機制,樣品不需要具有透明性質,探測儀器也不需要從樣品背部測量透射光的輻照度,這技術還可以應用於吸光度極高的物質,並且不具有破壞性,只需要很少量的樣品就可以做測量。
橢圓偏振測量術也可以用來測量薄膜的複折射率與厚度。應用橢圓偏振技術,照射光束於薄膜樣品,然後分析反射光的偏振改變,即可估算複數折射率或介電函數張量,以此獲得基本的物理參數,這包括表面粗糙度(roughness)、晶體質量、化學成分或導電性。它常被用來鑑定單層或多層堆疊的薄膜厚度,可量測厚度由數Å到幾微米,甚至小至一個單原子層,並且準確性極高。[4]:585ff[21]:632
地質學

火山 沙粒的顯微照片;上圖使用的是平面偏振光,下圖是偏光儀。在中間靠左位置的尺寸塊寬度為0.25 mm。
很多晶體礦石具有線性雙折射性質,這促成了偏振現象的初始發現。在礦物學裏,偏振顯微鏡時常會應用這雙折射性質來辨識礦石。更詳盡說明,請參閱光學礦物學(optical mineralogy)。[22]:163-164
地震學
在地震學裏,地震波主要分為兩種,一種是面波,一種是體波。面波傳播於地球表面,體波傳播於地球內部。體波又分成縱波和橫波兩種:[23]:48-50[13]:56-57
- 縱波在這裡被稱為P波,P代表主要(primary)或壓強(pressure),縱波是一種壓縮波,粒子振動方向平行於地震波的前進方向,在所有地震波中,它的前進速度最快,也最早抵達地表。P波能傳播於固體、液體或氣體。
- 橫波在這裡被稱為S波,S意指次要(secondary)或剪切力(shear),橫波是一種剪切波(shear wave),粒子振動方向垂直於地震波的前進方向,它的前進速度僅次於P波。S波只能在固體中傳播,由於地球外核呈液態,S波無法穿過外核。
由於P波和S波的傳播速度不同,利用兩者之間的走時差,可作簡單的地震定位。
化學
根据平面偏振光通過由手性物質時偏振平面旋轉的方向,可以將手性物質的對映異構體分類為左旋、右旋兩種;朝著光源望去,左旋對映異構體會使得偏振平面朝著逆時針方向旋轉,右旋對映異構體會使得偏振平面朝著順時針方向旋轉。這種偏振平面被旋轉的現象,稱為「圓雙折射現象」,能夠造成這種現象的物質稱為光學活性物質。由於這兩種手性物質裏的每一個化學鍵的性質與能量都相同,兩種物質的沸點、熔點、密度等等都一樣,應用圓雙折射現象,可以辨識手性物質的種類到底是左旋還是右旋。
假若在樣品溶液內,左旋與右旋對映異構體的數量相等(稱這種樣品為外消旋混合物),則它們各自產生的效應會相互抵銷,不會產生圓雙折射現象;假若只有一種對映異構體,或者其中某種對映異構體數量較多,則會出現圓雙折射現象(或旋光性,光學活性),從而顯示出不平衡程度的大小(或者物質的濃度,假若只有一種對映異構體存在)。偏振計可以用來量度這種現象。偏振計裏面有一個起偏器與一個檢偏器。將起偏器製成的偏振光入射於光學活性液體,使偏振光被旋轉有限角度,調整檢偏器的旋轉角度,當透射過檢偏器的光強變得最大之時,檢偏器的旋轉角度可以用來估算光學活性液體所造成的旋轉角度。液體樣品的旋光率(specific rotation)等於旋轉角度除以樣品長度。[6]:169-172
天文學
恆星分光偏振譜儀(stellar spectropolarimeter)可以用來測量恆星的磁場,這種儀器是攝譜儀和偏振計的結合。第一個來研究恆星磁場的儀器命名為「NARVAL」,被安裝在法國比利牛斯山比格爾地區的貝爾納·李奧望遠鏡上[24]。
雖然關於恆星熱輻射的研究通常不會涉及到偏振,很多相干性天文輻射源會發射出偏振輻射,例如羥基微波激射、甲醇微波激射等等天体微波激射(astrophysical maser),另外,星際塵埃也會藉著散射機制將星光偏振化。對於這些偏振輻射做偏振測量可以給出關於輻射源、輻射源附近恆星形成的區域關於磁場的信息。[25]:119,124由於地球與太陽的磁場超強於星際磁場,普通方法無法直接地測量到星際磁場;必需使用特別方法,例如,可以應用法拉第效應來測量星際磁場。從遙遠輻射源發射出的偏振射電輻射,其偏振平面因法拉第效應產生的旋轉角度與磁場成正比。使用這種方法測量到星際磁場大約為10-10-10-9T。[26]:336-337
宇宙微波背景的偏振可以用來研究宇宙暴脹的各種物理行為,特別是宇宙暴脹產生的引力輻射與能量尺寸(1015–1016GeV) 。[27][28]這是普朗克衛星的重要任務之一。[29]
天文學者认为,天文輻射很可能促成了地球生物分子的手性。[30]
重要應用
偏光太陽鏡

起偏器對於從淤泥灘的反射光所產生的效應:左圖顯示出,偏振軸與水平線平行的起偏器會透射這些反射光;右圖顯示出,旋轉這起偏器90°會阻擋幾乎全部鏡面反射光,如同使用偏光太陽鏡。[6]:348-350
照射非偏振光於鏡面表面(光亮表面),通常得到的反射光會具有某種程度的偏振。1808年,法國物理學者艾蒂安-路易·馬呂斯最先觀察到這現象。偏光太陽鏡利用這效應來降低水平表面反射出來的眩光,特別是當太陽從前方斜照下來時,張眼往前方路面望去會看到的強勁眩光。[6]:348-350
天空中的偏振光

右邊照片顯示出偏振濾光片對於天空景色產生的效應。
傳播於地球大氣層的太陽光會因為被大氣分子瑞利散射而使得散射光產生偏振,從天空中的散射光可以觀察到這現象。散射光在清晰的天空中會顯得更明亮、更具色彩。在天空中,與太陽照射的光束呈直角方向的位置,最容易觀察到這偏振現象(偏振方向與太陽光方向、直角方向相垂直)。這種具有部分偏振的散射光,假若使用起偏器,可以使得照片裏的天空變得較黑,增加对比度(contrast);這樣,可以改良照片的品質。[6]:346-347[31]:495-499
出現在天空中的偏振光常被用來導航定向。從九世紀至十一世紀間,維京人時常航行於北大西洋。那時期,歐洲人尚未知道怎樣使用磁羅盤,維京人主要是使用太陽與星星來導航定向,可是,在陰天,這方法無效。學者猜測他們可能知道怎樣使用一種稱為「太陽石」(sunstone)的簡單儀器,但這爭議性理論尚未被證實。1950年代,運輸飛機航行在地磁極附近時,由於無法使用磁羅盤,假若無法看到太陽或星星時(例如,在陰天或黃昏),時常會使用「天空羅盤」(sky compass)來導航。這儀器是一種很精緻的偏光儀,可以用來觀測天空中的偏振光。十九世紀後期, 查理斯·惠斯通(Charles Wheatstone)發明了偏振鐘(polar clock)。這也是一種偏光儀,可以用來計時。根據惠斯通,偏振鐘比日晷的優點更多。[32]:65-69
液晶顯示器

上方:电路断开,液晶亮。
下方:回路接通,液晶不亮。
液晶顯示器(LCD)科技倚賴液晶來旋轉偏振光的偏振平面。如右圖所示,在兩塊正交平面偏振片P1、P2之間置入透明電極層E1、E2和扭曲向列型液晶LC。照射非偏振光L於偏振片P1,透射光會呈平面偏振。[6]:370-373
- 上方圖:當E1、E2不通電時,液晶分子會呈螺旋狀排列,平面偏振光的偏振平面會被液晶LC逐漸扭曲,因此平面偏振光才能透射過正交的偏振片P2。假設安裝鏡子I,則透射過的平面偏振光會被反射回來(注意到顯示於鏡子的反射光箭頭),其偏振平面會再被液晶朝反方向扭曲,因此才能透射過正交的偏振片P1。從初始發光源位置朝著偏振片P1望去,會觀察到明亮的反射光。
- 下方圖:當電極E1、E2通電時,液晶分子會順著電場方向排列,因此液晶不會扭曲平面偏振光的偏振平面,由於兩塊偏振片的偏振軸相互垂直,這時光線不能透射過偏振片P2。雖然安裝鏡子I,從原先發光源位置朝著平面偏振片P1望去,仍舊不會觀察到任何反射光。
應用這機制,液晶顯示器能夠顯示簡單的文字或圖案信息,它的主要優點是功耗較低,因此可以使用光電池來供電。
三維電影
三維電影所使用的立體顯示技術將兩個不同影像分別傳輸至左眼、右眼。現今,這技術的首選方法是「偏振編碼」;使用兩台投影機將兩個不同影像都投射到投影屏,每一台投影機都安裝了偏振軸相互垂直的起偏器;或者使用單台能夠時分復用偏振的投影機(內部安裝了快速過濾交替偏振的元件)。三維眼鏡的左邊鏡片與右邊鏡片分別具有對應的檢偏器,確使每一隻眼睛只會接收到對應的偏振影像。早先,採用平面偏振編碼,因為費用較便宜、分離效果很好。但是,圓偏振所形成的分離影像不會受到觀眾頭部傾斜的影響。現今,三維電影已廣泛採用圓偏振技術,例如RealD 戲院系統。圓偏振技術需要使用特殊的投影屏,例如「銀屏」(silver screen),這種投影屏能夠維持投射影像的圓偏振,不會在反射時被非偏振化;普通的白色漫反射投影屏會造成投射影像在反射時被非偏振化,無法用來展示三維電影。[33][34]
動物視覺
很多種動物可以感視到偏振光的光強與方向。通常牠們會用這能力來導航。很多種昆蟲也具有這種辨識偏振光的能力,包括蜜蜂在內,蜜蜂用來表達食物源方向的舞蹈就是用這信息來定向。[32]:102-103生物學者經過仔細研究發覺,章魚、魷魚、烏賊、蝦蛄可以感視到偏振光。生物學者猜想,章魚、魷魚、烏賊使用這能力來探測會反射光的魚。有些魚會用反射光機制來掩飾自己。但是反射光的偏振與海水的散射偏振不同,因此魚的這種掩飾可以被破解。烏賊的快速變化、鮮艷顏色、具有偏振功能的表皮圖案,可以用來彼此傳達信息。[32]:111-112某種蝦蛄能夠觀察偏振的所有六個正交分量(水平、垂直、對角、反對角、左旋圓、右旋圓),被認為具有最優化的偏振視覺。[35]信鴿被認為能夠感視到天空的偏振光,這種能力可以幫助牠們遠距離歸巢。但是,嚴格做實驗檢驗證實這純屬謠傳。[36]
假若不藉用任何濾光器,則人的肉眼對於偏振光的視覺非常微弱。偏振光會在視場中心附近造成很模糊的圖樣,稱為海丁格刷(Haidinger's brush)。這種圖樣非常難看到,但若經過一番練習,人可以用他的肉眼觀察到偏振光。[32]:118
圓偏振的角動量
電磁輻射朝著傳播方向帶有線性動量。另外,圓偏振光還帶有角動量。與動量相比,這角動量非常小,很難測得。可是,在一個很值得注意的實驗裏,應用這性質,達成了令人難以想像的高旋轉速度。
英國聖安德魯斯大學實驗團隊使得一個直徑4微米的微觀尺度碳酸鈣圓球以每分鐘6億圈速度旋轉。應用光鑷技術,這個圓球被圓偏振激光束懸浮起來。由於碳酸鈣圓球具有雙折射性質,透射光的偏振度(degree of polarization)會被降低,因此失去一些角動量給圓球。被懸浮於幾乎真空,遭受到微乎其微的摩擦力,圓球的旋轉速度可以增加至每分鐘6億圈。這旋轉速度對應於離心加速度大約為地球表面重力的10億倍,但是令人驚奇的是,圓球並沒有因此被擊碎。[37][38]
參見
- 消偏器
- 徑向偏振
- 偏振片
- 克爾效应
- 泡克耳斯效应
- 偏振光显微镜
註釋
^ 一般而言,在實際介質裏,由於介質的耗散性質或擁有自由電荷,電磁波不是橫波。[6]:46
^ 在這裡,簡單介質指的是自由空間或均勻(homogeniety)、各向同性、非衰減性(non-attenuating)介質
^ 回想在瓊斯向量與瓊斯矩陣段落的橫電磁波
E(z,t)=(E0xeiφx,E0yeiφy)ei(kz−ωt){displaystyle mathbf {E} (z,t)=left(E_{0x}e^{ivarphi _{x}},,E_{0y}e^{ivarphi _{y}}right)e^{i(kz-omega t)}},
這橫電磁波的斯托克斯向量為
S=(S0S1S2S3)=(E0x2+E0y2E0x2−E0y22E0xE0ycosφ2E0xE0ysinφ){displaystyle mathbf {S} ={begin{pmatrix}S_{0}\S_{1}\S_{2}\S_{3}\end{pmatrix}}={begin{pmatrix}E_{0x}^{2}+E_{0y}^{2}\E_{0x}^{2}-E_{0y}^{2}\2E_{0x}E_{0y}cos varphi \2E_{0x}E_{0y}sin varphi \end{pmatrix}}}。
參考文獻
^ 1.01.1 Whittaker, E. T., A history of the theories of aether and electricity. Vol 1, Nelson, London, 1951
^ 2.02.1 Ronald G. Driggers. Encyclopedia of Optical Engineering. CRC Press. ISBN 978-0-8247-4252-2.
^ 3.03.1 Jed Z. Buchwald; Robert Fox. The Oxford Handbook of the History of Physics. Oxford University Press. October 2013. ISBN 978-0-19-969625-3.
^ 4.04.14.24.34.4 Dennis Goldstein; Dennis H. Goldstein. Polarized Light, Revised and Expanded. CRC Press. 3 January 2011. ISBN 978-0-203-91158-7.
^ 5.05.1 Joseph W. Goodman. Introduction to Fourier Optics. Roberts and Company Publishers. 2005. ISBN 978-0-9747077-2-3.
^ 6.006.016.026.036.046.056.066.076.086.096.106.116.12 Hecht, Eugene, Optics 4th, United States of America: Addison Wesley, 2002, ISBN 0-8053-8566-5 (英语)
^ Jackson, John David, Classical Electrodynamic 3rd., USA: John Wiley & Sons, Inc.: pp. 1–2, 1999, ISBN 978-0-471-30932-1 引文格式1维护:冗余文本 (link)
^ Subrahmanyan Chandrasekhar. Radiative Transfer. Dover Publications. 15 April 2013. ISBN 978-0-486-31845-5.
^ Michael North. Principles and Applications of Stereochemistry. CRC Press. ISBN 978-0-7487-3994-3.
^ 10.010.1 Griffiths, David J., Introduction to Electrodynamics (3rd ed.), Prentice Hall, 1998, ISBN 0-13-805326-X
^ Geoffrey New. Introduction to Nonlinear Optics. Cambridge University Press. 7 April 2011. ISBN 978-1-139-50076-0.
^ Dorn, R. and Quabis, S. and Leuchs, G. Sharper Focus for a Radially Polarized Light Beam. Physical Review Letters. dec 2003, 91 (23,): 233901–+. Bibcode:2003PhRvL..91w3901D. doi:10.1103/PhysRevLett.91.233901. 请检查|date=中的日期值 (帮助)
^ 13.013.1 Seth Stein; Michael Wysession. An Introduction to Seismology, Earthquakes, and Earth Structure. John Wiley & Sons. 1 April 2009. ISBN 978-1-4443-1131-0.
^ Griffiths, David J., Introduction to Elementary Particles 2nd revised, WILEY-VCH, 2008, ISBN 978-3-527-40601-2
^ Bernard Schutz. A First Course in General Relativity. Cambridge University Press. 14 May 2009. ISBN 978-0-521-88705-2.
^ 16.016.116.216.3 Edward Collett. Field Guide to Polarization. Society of Photo Optical. 2005. ISBN 978-0-8194-5868-1.
^ 17.017.117.2 What is Polarisation (PDF). Polarimetry Tutorial. European Space Agency. (原始内容 (PDF)存档于2014-02-24).
^ Edward Collett. Polarized Light in Fiber Optics. SPIE Press. 2003. ISBN 978-0-8194-5761-5.
^ Edward L. O'Neill. Introduction to Statistical Optics. Courier Dover Publications. January 2004. ISBN 978-0-486-43578-7.
^ Srinivasan, M. R. Physics for Engineers. New Age International. 1 January 1996. ISBN 978-81-224-0892-8.
^ Masud Mansuripur. Classical Optics and Its Applications. Cambridge University Press. 2009. ISBN 978-0521881692.
^ Randy O. Wayne. Light and Video Microscopy. Academic Press. 16 December 2013. ISBN 978-0-12-411536-1.
^ Peter M. Shearer. Introduction to Seismology. Cambridge University Press. 2009. ISBN 978-0-521-88210-1.
^ Staff. NARVAL: First Observatory Dedicated To Stellar Magnetism. Science Daily. February 22, 2007 [2007-06-21].
^ Vlemmings, W. H. T. A review of maser polarization and magnetic fields. (PDF). Proceedings of the International Astronomical Union. Mar 2007, 3 (S242): 37–46.
^ Hannu Karttunen; Pekka Kröger; Heikki Oja. Fundamental Astronomy. Springer. 27 June 2007. ISBN 978-3-540-34143-7.
^ Boyle, Latham A.; Steinhardt, PJ; Turok, N. Inflationary predictions for scalar and tensor fluctuations reconsidered. Physical Review Letters. 2006, 96 (11): 111301. Bibcode:2006PhRvL..96k1301B. PMID 16605810. arXiv:astro-ph/0507455. doi:10.1103/PhysRevLett.96.111301.
^ Tegmark, Max. What does inflation really predict?. JCAP. 2005, 0504 (4): 001. Bibcode:2005JCAP...04..001T. arXiv:astro-ph/0410281. doi:10.1088/1475-7516/2005/04/001.
^ Planck: The Scientific Programme (PDF). European Space Agency. 2005 [6 March 2009]. ESA-SCI(2005)1.
^ Clark, S. Polarised starlight and the handedness of Life. American Scientist. 1999, 97: 336–43. Bibcode:1999AmSci..87..336C. doi:10.1511/1999.4.336.
^ Bekefi, George; Barrett, Alan, Electromagnetic Vibrations, Waves, and Radiation, USA: MIT Press, 1977, ISBN 0-262-52047-8
^ 32.032.132.232.3 J. David Pye. Polarised Light in Science and Nature. CRC Press. 13 February 2001. ISBN 978-0-7503-0673-7.
^ Verrier, Richard. 3-D technology firm RealD has starring role at movie theaters. Los Angeles Times. 2009-03-26 [2011-02-05].
^ Cowan, Matt. Real D 3D Theatrical System (PDF). European Digital Cinema Forum. [2009-03-28].
^ Sonja Kleinlogel, Andrew White. The secret world of shrimps: polarisation vision at its best. PLoS ONE. 2008, 3 (5): e2190. Bibcode:2008PLoSO...3.2190K. PMC 2377063. PMID 18478095. arXiv:0804.2162. doi:10.1371/journal.pone.0002190.
^ "No evidence for polarization sensitivity in the pigeon electroretinogram", J. J. Vos Hzn, M. A. J. M. Coemans & J. F. W. Nuboer, The Journal of Experimental Biology, 1995.
^ University of St Andrews scientists create 'fastest man-made spinning object'. BBC News. Aug 28, 2013 [May 6, 2014].
^ Yoshihiko, Arita; Mazilu, Michael; Dholakia, Kishan. Laser-induced rotation and cooling of a trapped microgyroscope in vacuum. Nature Communications. Aug 28, 2013, 4 [May 6, 2014]. doi:10.1038/ncomms3374.
| ||||||||||||||||||||||||||||||||||||
|