Cfxtrjtrk

本条目翻譯品質不佳。 翻譯者可能不熟悉中文或原文語言，也可能使用了機器翻譯，請協助翻譯本條目或重新編寫，并注意避免翻译腔的问题。明顯拙劣的機器翻譯請改掛{{Delete|G13}}提交刪除。

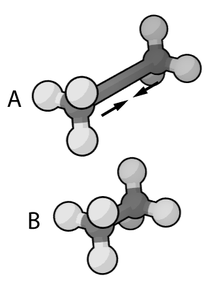
A force field is used to minimize the bond stretching energy of this ethane molecule.

分子力学采用经典力学来模拟分子体系。在分子力学中，使用分子力场方法计算出所有系统的势能。分子力学可用于研究小分子，也可用于研究具有成千乃至上百万原子数的大型生物系统或材料。

全原子分子力学方法具有以下性质：

• 将每个原子模拟为单个粒子


• 每个粒子具有一个半径值（通常为范德华半径），极化率和一个恒定的净电荷数（通常来自于量子计算和/或实验）


• 将原子间互相成键作用模拟为“连线”，取平衡距离等于实验或计算所得的键长

这个方法有几个可能的变体。例如，许多模拟方法曾使用“原子团”模型（此模型将一个甲基基团或亚甲基单元视为单个粒子），而大型蛋白系统则通常使用“珠”模型（此模型将一个氨基酸视为二至四个粒子）进行模拟。

函数形式

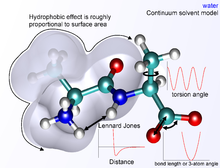
Molecular mechanics potential energy function with continuum solvent.

下文中的函数（即化学势函数，或称化学力场函数），用于在给定的构象下，对独立能量进行加和，计算分子体系的势能（E）。

 E=Ecovalent+Enoncovalent{displaystyle E=E_{text{covalent}}+E_{text{noncovalent}},}

其中，共价键和非共价键的贡献由下面的和式求出：

 Ecovalent=Ebond+Eangle+Edihedral{displaystyle E_{text{covalent}}=E_{text{bond}}+E_{text{angle}}+E_{text{dihedral}}}

 Enoncovalent=Eelectrostatic+Evan der Waals{displaystyle E_{text{noncovalent}}=E_{text{electrostatic}}+E_{text{van der Waals}}}

分子体系的确切的势能函数形式，或其分子力场形式，取决于所使用的特定的仿真程序。

应用领域

分子力学的一个应用是能量最小化。换句话说，将 力场原则用作 优化 准则，通过适当算法（如 最速下降法）寻找（局部）最小值。

环境和溶剂化

软件包

这个列表不完整。有许多列表中未包含的软件可以用于进行分子力学模拟的计算。

相关条目

参考文献

• 
  Allinger NL, Burkert U. Molecular Mechanics. An American Chemical Society Publication. 1982. ISBN 0-8412-0885-9. 
  


• 
  Box VG. The Molecular Mechanics of Quantized Valence Bonds. J Mol Model. March 1997, 3 (3): 124–41. doi:10.1007/s008940050026. 
  


• 
  Box VG. The anomeric effect of monosaccharides and their derivatives. Insights from the new QVBMM molecular mechanics force field. Heterocycles. 12 November 1998, 48 (11): 2389–417. doi:10.3987/REV-98-504. 
  


• 
  Box VG. Stereo-electronic effects in polynucleotides and their double helices. J Mol Struct. 2004, 689 (1–2): 33–41. Bibcode:2004JMoSt.689...33B. doi:10.1016/j.molstruc.2003.10.019. 
  


• 
  Becker OM. Computational biochemistry and biophysics. New York, N.Y.: Marcel Dekker. 2001. ISBN 0-8247-0455-X. 
  


• 
  Mackerell AD. Empirical force fields for biological macromolecules: overview and issues. J Comput Chem. October 2004, 25 (13): 1584–604. PMID 15264253. doi:10.1002/jcc.20082. 
  


• 
  Schlick T. Molecular modeling and simulation: an interdisciplinary guide. Berlin: Springer. 2002. ISBN 0-387-95404-X. 
  


• 
  Krishnan Namboori; Ramachandran, K. S.; Deepa Gopakumar. Computational Chemistry and Molecular Modeling: Principles and Applications. Berlin: Springer. 2008. ISBN 3-540-77302-9. ^[1]
  

外部链接

• Molecular dynamics simulation methods revised


• Molecular mechanics - it is simple